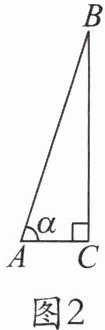
7. 如图 1,梯子斜靠在竖直的墙上,其示意图如图 2,梯子与地面所成的角 $ \alpha $ 为 $ 75^{\circ} $,梯子 $ AB $ 长 $ 3 m $,求梯子顶部离地竖直高度 $ BC $。(结果精确到 $ 0.1 m $,参考数据:$ \sin 75^{\circ} \approx 0.97 $,$ \cos 75^{\circ} \approx 0.26 $,$ \tan 75^{\circ} \approx 3.73 $)



答案:
7.解:在$Rt\triangle ABC$中,AB=3,$\angle ACB=90^{\circ},$$\angle BAC=75^{\circ},$
$\therefore BC=AB \cdot \sin75^{\circ} \approx 3 × 0.97 = 2.91 \approx 2.9(m)。$
答:梯子顶部离地竖直高度BC约为2.9m。
$\therefore BC=AB \cdot \sin75^{\circ} \approx 3 × 0.97 = 2.91 \approx 2.9(m)。$
答:梯子顶部离地竖直高度BC约为2.9m。
8. (1) 通过计算(可用计算器)比较大小,并提出你的猜想:
① $ \sin 30^{\circ} $
② $ \sin 36^{\circ} $
③ $ \sin 45^{\circ} $
④ $ \sin 60^{\circ} $
⑤ $ \sin 80^{\circ} $
猜想:若 $ 0^{\circ} < \alpha < 45^{\circ} $,则 $ \sin 2\alpha $
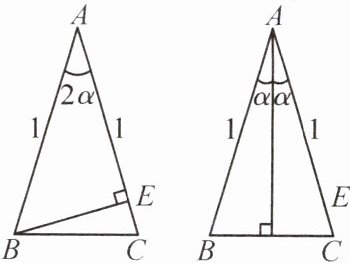
(2) 已知:如图,在 $ \triangle ABC $ 中,$ AB = AC = 1 $,$ \angle BAC = 2\alpha $。请根据图中的提示,利用面积法检验你的结论。
① $ \sin 30^{\circ} $
=
$ 2 \sin 15^{\circ} \cos 15^{\circ} $;② $ \sin 36^{\circ} $
=
$ 2 \sin 18^{\circ} \cos 18^{\circ} $;③ $ \sin 45^{\circ} $
=
$ 2 \sin 22.5^{\circ} \cos 22.5^{\circ} $;④ $ \sin 60^{\circ} $
=
$ 2 \sin 30^{\circ} \cos 30^{\circ} $;⑤ $ \sin 80^{\circ} $
=
$ 2 \sin 40^{\circ} \cos 40^{\circ} $。猜想:若 $ 0^{\circ} < \alpha < 45^{\circ} $,则 $ \sin 2\alpha $
=
$ 2 \sin \alpha \cos \alpha $。(2) 已知:如图,在 $ \triangle ABC $ 中,$ AB = AC = 1 $,$ \angle BAC = 2\alpha $。请根据图中的提示,利用面积法检验你的结论。

答案:
8.
(1)= = = = = =。
$(2)\because S_{\triangle ABC} = \frac{1}{2}AC \cdot BE = \frac{1}{2} × 1 × \sin2\alpha = \frac{1}{2}\sin2\alpha,$
$S_{\triangle ABC} = \frac{1}{2}BC \cdot AD = BD \cdot AD = \sin\alpha \cdot \cos\alpha,$
$\therefore \frac{1}{2}\sin2\alpha = \sin\alpha \cdot \cos\alpha,$即$\sin2\alpha = 2\sin\alpha\cos\alpha。$
(1)= = = = = =。
$(2)\because S_{\triangle ABC} = \frac{1}{2}AC \cdot BE = \frac{1}{2} × 1 × \sin2\alpha = \frac{1}{2}\sin2\alpha,$
$S_{\triangle ABC} = \frac{1}{2}BC \cdot AD = BD \cdot AD = \sin\alpha \cdot \cos\alpha,$
$\therefore \frac{1}{2}\sin2\alpha = \sin\alpha \cdot \cos\alpha,$即$\sin2\alpha = 2\sin\alpha\cos\alpha。$
查看更多完整答案,请扫码查看


