3. 已知抛物线 $ y = x^{2} + ax + b $ 与 $ x $ 轴交于 $ A(1,0) $,$ B(3,0) $ 两点,与 $ y $ 轴交于点 $ C $.
(1) 填空:$ a = $
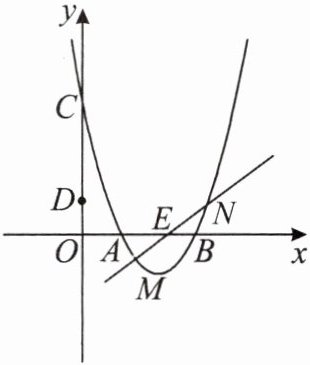
(2) 如图,已知点 $ E(\frac{5}{2},0) $,过点 $ E $ 的直线与抛物线交于点 $ M $,$ N $,且点 $ M $,$ N $ 关于点 $ E $ 对称,求直线 $ MN $ 的表达式.
(1) 填空:$ a = $
-4
,$ b = $3
.(2) 如图,已知点 $ E(\frac{5}{2},0) $,过点 $ E $ 的直线与抛物线交于点 $ M $,$ N $,且点 $ M $,$ N $ 关于点 $ E $ 对称,求直线 $ MN $ 的表达式.

答案:
3.解:
(1)-4,3.
(2)由
(1)得抛物线解析式为$ y=x^{2}-4x+3,$设 M,N 的横坐标为 m,n,直线 MN 过点$ E(\frac{5}{2},0),$
设直线 MN 的解析式为$ y=k(x-\frac{5}{2}),$联立两个解析式并整理,得$ x^{2}-(4+k)x+(3+\frac{5}{2}k)=0,$则 m+n=4+k,
∵点 M,N 关于点 E 对称,则$ m+n=2×\frac{5}{2}=5,$
∴k=1,即直线 MN 的解析式为$ y=x-\frac{5}{2}.$
(1)-4,3.
(2)由
(1)得抛物线解析式为$ y=x^{2}-4x+3,$设 M,N 的横坐标为 m,n,直线 MN 过点$ E(\frac{5}{2},0),$
设直线 MN 的解析式为$ y=k(x-\frac{5}{2}),$联立两个解析式并整理,得$ x^{2}-(4+k)x+(3+\frac{5}{2}k)=0,$则 m+n=4+k,
∵点 M,N 关于点 E 对称,则$ m+n=2×\frac{5}{2}=5,$
∴k=1,即直线 MN 的解析式为$ y=x-\frac{5}{2}.$
4. 如图,二次函数 $ y = (x - 1)(x - a) $($ a $ 为常数)的图象的对称轴为直线 $ x = 2 $.
(1) 求 $ a $ 的值.
(2) 向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.

(1) 求 $ a $ 的值.
(2) 向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.

答案:
4.解:
(1)抛物线与 x 轴的交点坐标是(1,0)和(a,0).
∵对称轴为直线 x=2,
∴$\frac{1+a}{2}=2,$解得 a=3.
(2)由
(1)知,a=3,则该抛物线表达式是$ y=x^{2}-4x+3,$
∵抛物线向下平移 3 个单位后经过原点,
∴平移后图象所对应的二次函数的表达式是$ y=x^{2}-4x.$
(1)抛物线与 x 轴的交点坐标是(1,0)和(a,0).
∵对称轴为直线 x=2,
∴$\frac{1+a}{2}=2,$解得 a=3.
(2)由
(1)知,a=3,则该抛物线表达式是$ y=x^{2}-4x+3,$
∵抛物线向下平移 3 个单位后经过原点,
∴平移后图象所对应的二次函数的表达式是$ y=x^{2}-4x.$
查看更多完整答案,请扫码查看


