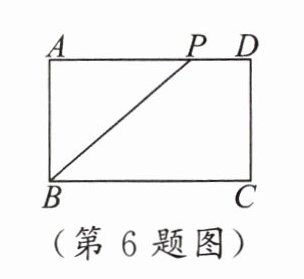
6. 如图,已知在矩形 $ ABCD $ 中,$ AB = 1 $,$ BC = \sqrt{3} $,$ P $ 是边 $ AD $ 上的一个动点,连结 $ BP $,点 $ C $ 关于直线 $ BP $ 的对称点为 $ C_1 $,当点 $ P $ 运动时,点 $ C_1 $ 也随之运动。若点 $ P $ 从点 $ A $ 运动到点 $ D $,则线段 $ CC_1 $ 扫过的区域的面积是(
A.$ \pi $
B.$ \pi + \frac{3\sqrt{3}}{4} $
C.$ \frac{3\sqrt{3}}{2} $
D.$ 2\pi $
B
)
A.$ \pi $
B.$ \pi + \frac{3\sqrt{3}}{4} $
C.$ \frac{3\sqrt{3}}{2} $
D.$ 2\pi $
答案:
6.B
7. 如图,把半径为 $ 1 $ 的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图所示的恒星图形,那么这个恒星图形的面积等于
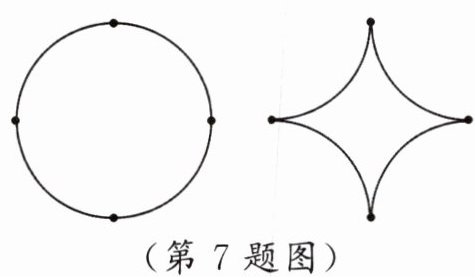
4−π
。
答案:
7.4−π
8. 如图,在矩形 $ ABCD $ 中,$ AB = 2\ cm $,$ AD = \sqrt{3}\ cm $,以点 $ B $ 为圆心、$ AB $ 长为半径画弧,交 $ CD $ 于点 $ E $。求图中阴影部分的面积。
 ]
]
 ]
]
答案:
8.解:连结BE,如图所示,由题意,得BE=AB=2cm,
∵四边形ABCD是矩形,
∴∠ABC = ∠C = 90°,
∵AD = $\sqrt{3}$cm,
∴EC = 1 cm,
∴∠EBC = 30°,
∠ABE = 60°,
∴S_{阴影} = S_{矩形ABCD} - S_{扇形ABE} - S_{\triangle ECB} =
2$\sqrt{3}$ - $\frac{60 × 2^{2}\pi}{360}$ - $\frac{\sqrt{3}}{2}$ = ($\frac{3\sqrt{3}}{2}$ - $\frac{2\pi}{3}$) cm².

8.解:连结BE,如图所示,由题意,得BE=AB=2cm,
∵四边形ABCD是矩形,
∴∠ABC = ∠C = 90°,
∵AD = $\sqrt{3}$cm,
∴EC = 1 cm,
∴∠EBC = 30°,
∠ABE = 60°,
∴S_{阴影} = S_{矩形ABCD} - S_{扇形ABE} - S_{\triangle ECB} =
2$\sqrt{3}$ - $\frac{60 × 2^{2}\pi}{360}$ - $\frac{\sqrt{3}}{2}$ = ($\frac{3\sqrt{3}}{2}$ - $\frac{2\pi}{3}$) cm².

查看更多完整答案,请扫码查看


