《2025年名师面对面学科素养评价九年级数学全一册浙教版》

1. 如图，在$\triangle ABC$中，$DE// BC$，$\frac{AD}{DB}=\frac{2}{3}$。若$AC = 6$，则$EC=$(C)

A.$\frac{6}{5}$
B.$\frac{12}{5}$
C.$\frac{18}{5}$
D.$\frac{24}{5}$

答案： 1.C

2. 如图，$AB// CD$，$AC$，$BD$相交于点$E$，$AE = 1$，$EC = 2$，$DE = 3$，则$BD$的长为(C)

A.$\frac{3}{2}$
B.$4$
C.$\frac{9}{2}$
D.$6$

答案： 2.C

3. 如图，$l_1// l_2// l_3$，两条直线与这三条平行线分别交于点$A$，$B$，$C$和$D$，$E$，$F$。已知$\frac{AB}{BC}=\frac{3}{2}$，则$\frac{DE}{DF}$的值为(D)

A.$\frac{3}{2}$
B.$\frac{2}{3}$
C.$\frac{2}{5}$
D.$\frac{3}{5}$

答案： 3.D

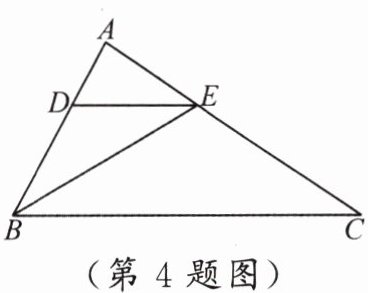
4. 如图，在$\triangle ABC$中，$BE$平分$\angle ABC$，$DE// BC$。若$DE = 2AD$，$AE = 2$，则$AC =$6。

答案： 4.6

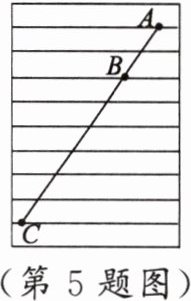
5. 如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点$A$，$B$，$C$都在横格线上。若线段$AB = 4\mathrm{cm}$，则线段$BC =$12$\mathrm{cm}$。

答案： 5.12

6. 如图，已知$AB// MN$，$BC// NG$。
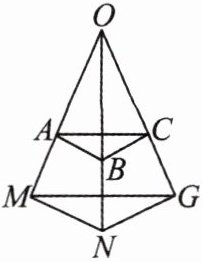
求证：$\frac{OA}{OM}=\frac{OC}{OG}$。

答案： 6.证明:
∵AB//MN,
∴$\frac{OA}{OM}$=$\frac{OB}{ON}$.
　又
∵BC//NG,
∴$\frac{OB}{ON}$=$\frac{OC}{OG}$.
∴$\frac{OA}{OM}$=$\frac{OC}{OG}$.