1. 如图,在$\triangle ABC$中,点$E$,$F$分别在边$AB$,$AC$上,$\angle 1=\angle 2$。若$BC = 4$,$AF = 2$,$CF = 3$,则$EF$的长为(

A.$2$
B.$3$
C.$\frac{5}{3}$
D.$\frac{8}{5}$
D
)
A.$2$
B.$3$
C.$\frac{5}{3}$
D.$\frac{8}{5}$
答案:
1.D
2. 已知平行四边形$ABCD$,点$E$是$DA$延长线上一点,则(

A.$\frac{AE}{AD}=\frac{AM}{CD}$
B.$\frac{AE}{AD}=\frac{EM}{MC}$
C.$\frac{BM}{CD}=\frac{BF}{BD}$
D.$\frac{ED}{BC}=\frac{AD}{BM}$
B
)
A.$\frac{AE}{AD}=\frac{AM}{CD}$
B.$\frac{AE}{AD}=\frac{EM}{MC}$
C.$\frac{BM}{CD}=\frac{BF}{BD}$
D.$\frac{ED}{BC}=\frac{AD}{BM}$
答案:
2.B
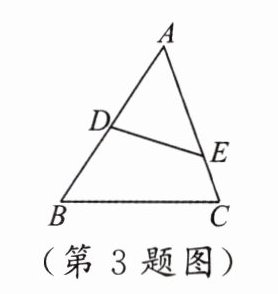
3. 如图,在$\triangle ABC$中,若$\angle AED=\angle B$,$DE = 6$,$AB = 10$,$AE = 8$,则$BC$的长为(
A.$\frac{15}{4}$
B.$7$
C.$\frac{15}{2}$
D.$\frac{24}{5}$
C
)
A.$\frac{15}{4}$
B.$7$
C.$\frac{15}{2}$
D.$\frac{24}{5}$
答案:
3.C
4. 如图,已知$\angle 1=\angle 2$,添加一个适当条件,使$\triangle ABC\backsim\triangle ADE$:

∠B = ∠D
,
答案:
4.∠B = ∠D
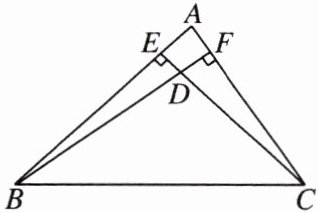
5. 如图所示,锐角$\triangle ABC$的边$AB$,$AC$上的高线$CE$和$BF$相交于点$D$,请写出图中的两对相似三角形:
△BDE∽△CDF,△ABF∽△ACE
。
答案:
5.△BDE∽△CDF,△ABF∽△ACE
6. 如图,在矩形$ABCD$中,$E$是$BC$的中点,$DF\perp AE$,垂足为$F$。
(1) 求证:$\triangle ABE\backsim\triangle DFA$。
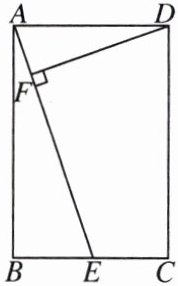
(2) 若$AB = 6$,$BC = 4$,求$DF$的长。
(1) 求证:$\triangle ABE\backsim\triangle DFA$。

(2) 若$AB = 6$,$BC = 4$,求$DF$的长。

答案:
6.解:
(1)
∵四边形ABCD是矩形,
∴AD//BC,∠B = 90°,
∴∠DAF = ∠AEB,
∵DF⊥AE,
∴∠AFD = ∠B = 90°,
∴△ABE∽△DFA.
(2)AE = $\sqrt{AB^2 + BE^2} = \sqrt{6^2 + 2^2} = 2\sqrt{10}$
∵△ABE∽△DFA,
∴$\frac{AB}{DF} = \frac{AE}{AD}$,
∴DF = $\frac{AB \cdot AD}{AE} = \frac{6 × 4}{2\sqrt{10}} = \frac{6}{5}\sqrt{10}$.
(1)
∵四边形ABCD是矩形,
∴AD//BC,∠B = 90°,
∴∠DAF = ∠AEB,
∵DF⊥AE,
∴∠AFD = ∠B = 90°,
∴△ABE∽△DFA.
(2)AE = $\sqrt{AB^2 + BE^2} = \sqrt{6^2 + 2^2} = 2\sqrt{10}$
∵△ABE∽△DFA,
∴$\frac{AB}{DF} = \frac{AE}{AD}$,
∴DF = $\frac{AB \cdot AD}{AE} = \frac{6 × 4}{2\sqrt{10}} = \frac{6}{5}\sqrt{10}$.
7. 在$\triangle ABC$中,$P$是$AB$上的动点($P$异于$A$,$B$),过点$P$的一条直线截$\triangle ABC$,使截得的三角形与$\triangle ABC$相似,我们不妨称这种直线为过点$P$的$\triangle ABC$的相似线。如图,$\angle A = 36^{\circ}$,$AB = AC$,当点$P$在$AC$的垂直平分线上时,过点$P$的$\triangle ABC$的相似线最多有

3
条。
答案:
7.3
查看更多完整答案,请扫码查看


