1. 如图,为了测量校园内旗杆 $ AB $ 的高度,九年级数学应用实践小组,根据光的反射定律,利用镜子、皮尺和测角仪等工具,按以下方式进行测量:把镜子放在点 $ O $ 处,然后观测者沿着水平直线 $ BO $ 后退到点 $ D $,这时恰好能在镜子里看到旗杆顶点 $ A $,此时测得观测者观看镜子的俯角 $ \alpha = 60^{\circ} $,观测者眼睛与地面距离 $ CD = 1.7 m $,$ BD = 11 m $,则旗杆 $ AB $ 的高度约为(结果取整数,$\sqrt{3} \approx 1.7$)(

A.$ 16 m $
B.$ 17 m $
C.$ 18 m $
D.$ 19 m $
B
)
A.$ 16 m $
B.$ 17 m $
C.$ 18 m $
D.$ 19 m $
答案:
1.B
2. 《孙子算经》有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影子长五寸。则竹竿的长为(提示:$ 1 $ 丈 $ = 10 $ 尺,$ 1 $ 尺 $ = 10 $ 寸)(
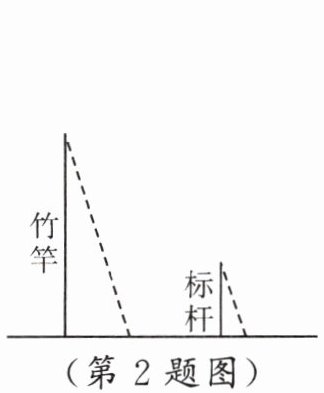
A.五丈
B.四丈五尺
C.一丈
D.五尺
B
)
A.五丈
B.四丈五尺
C.一丈
D.五尺
答案:
2.B
3. 如图,电灯 $ P $ 在横杆 $ AB $ 的正上方,$ AB $ 在灯光下的影子为 $ CD $,$ AB // CD $,$ AB = 2 m $,$ CD = 5 m $,点 $ P $ 到 $ CD $ 的距离是 $ 3 m $,则 $ P $ 到 $ AB $ 的距离是(
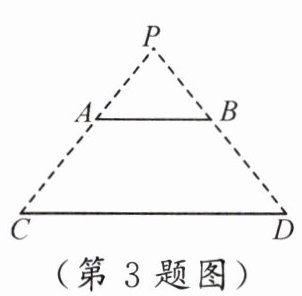
A.$ \dfrac{5}{6} m $
B.$ \dfrac{6}{7} m $
C.$ \dfrac{6}{5} m $
D.$ \dfrac{10}{3} m $
C
)
A.$ \dfrac{5}{6} m $
B.$ \dfrac{6}{7} m $
C.$ \dfrac{6}{5} m $
D.$ \dfrac{10}{3} m $
答案:
3.C
4. 如图,小明在 $ A $ 时测得某树的影长为 $ 8 m $,$ B $ 时又测得该树的影长为 $ 2 m $,若两次日照的光线互相垂直,则树的高度为

4
$ m $。
答案:
4.4
5. 下右图是夹文件用的铁(塑料)夹子在常态下的侧面示意图。$ AC $,$ BC $ 表示铁夹的两个面,$ O $ 点是轴,$ OD \perp AC $ 于点 $ D $。已知 $ AD = 15 mm $,$ DC = 24 mm $,$ OD = 10 mm $。已知文件夹是轴对称图形,求图中 $ A $,$ B $ 两点的距离。($\sqrt{676} = 26$)


答案:
5.解:连结AB,与CO延长线交于点E,由题意,得CE⊥AB,AE=EB.在Rt△AEC和Rt△ODC中,
∵∠AEC=∠ODC,∠OCD=∠ACE,
∴Rt△AEC∽Rt△ODC,
∴$\frac{AE}{AC} = \frac{OD}{OC}$,
又OC=$\sqrt{OD^{2} + DC^{2}} = \sqrt{10^{2} + 24^{2}} = 26$,
∴$AE = \frac{AC\cdot OD}{OC} = \frac{39 × 10}{26} = 15$,
∴AB=30(mm).
∵∠AEC=∠ODC,∠OCD=∠ACE,
∴Rt△AEC∽Rt△ODC,
∴$\frac{AE}{AC} = \frac{OD}{OC}$,
又OC=$\sqrt{OD^{2} + DC^{2}} = \sqrt{10^{2} + 24^{2}} = 26$,
∴$AE = \frac{AC\cdot OD}{OC} = \frac{39 × 10}{26} = 15$,
∴AB=30(mm).
查看更多完整答案,请扫码查看


