1. 已知$\triangle ABC$的三边长分别为$2,\sqrt{6},4$,$\triangle A'B'C'$的两边长分别是$\sqrt{2},\sqrt{3}$。如果$\triangle ABC$与$\triangle A'B'C'$相似,那么$\triangle A'B'C'$的第三边长应该是(
A.$6\sqrt{2}$
B.$4\sqrt{2}$
C.$3\sqrt{2}$
D.$2\sqrt{2}$
D
)A.$6\sqrt{2}$
B.$4\sqrt{2}$
C.$3\sqrt{2}$
D.$2\sqrt{2}$
答案:
1.D
2. 若两个相似三角形的相似比为$3:5$,则它们的对应角的角平分线的比为(
A.$1:3$
B.$3:5$
C.$1:5$
D.$9:25$
B
)A.$1:3$
B.$3:5$
C.$1:5$
D.$9:25$
答案:
2.B
3. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 12$,$BC = 5$,则此$Rt\triangle ABC$的重心$P$与外心$Q$之间的距离为(
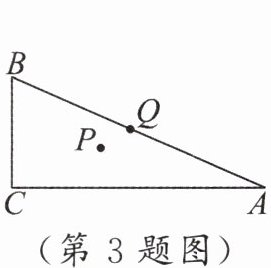
A.$\frac{13}{2}$
B.$\frac{13}{3}$
C.$\frac{13}{4}$
D.$\frac{13}{6}$
D
)
A.$\frac{13}{2}$
B.$\frac{13}{3}$
C.$\frac{13}{4}$
D.$\frac{13}{6}$
答案:
3.D
4. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$D$是边$AC$上一点,$\angle CBD = \angle A$,$E$,$F$分别是$AB$,$BD$的中点。若$AB = 5$,$AC = 4$,则$CF:CE=$
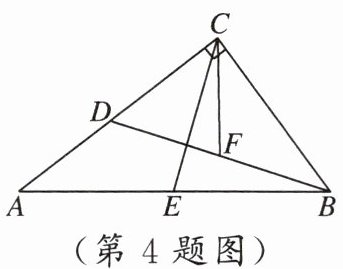
3:4
。
答案:
4.3:4
5. 如图,矩形$EFGH$内接于$\triangle ABC$,且边$FG$落在$BC$上。若$BC = 3$,$AD = 2$,$EF = \frac{2}{3}EH$,则$EH$的长为
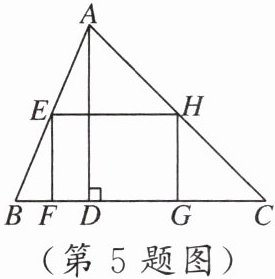
$\frac{3}{2}$
。
答案:
5.$\frac{3}{2}$
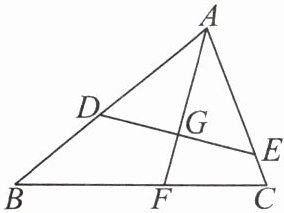
6. 如图,在$\triangle ABC$中,$D$,$E$分别是$AB$,$AC$上的点,$\angle AED = \angle B$,$AD = 2$,$AC = 3$,$\triangle ABC$的角平分线$AF$交$DE$于点$G$,交$BC$于点$F$。
(1) 求证:$\triangle ADE \sim \triangle ACB$。
(2) 求$\frac{AG}{GF}$的值。
]
(1) 求证:$\triangle ADE \sim \triangle ACB$。
(2) 求$\frac{AG}{GF}$的值。

]
答案:
6.
(1)证明:
∵∠AED=∠B,∠BAC=∠DAE,
∴△ADE∽△ACB.
(2)解:
∵△ADE∽△ACB,
∴∠ADE=∠C,
∵AF平分∠BAC,
∴∠DAG=∠CAF,
∴△ADG∽△ACF,
∴$\frac{AG}{AF}=\frac{AD}{AC}$,
∵AD=2,AC=3,
∴$\frac{AG}{AF}=\frac{2}{3}$,
∴$\frac{AG}{GF}=2$.
(1)证明:
∵∠AED=∠B,∠BAC=∠DAE,
∴△ADE∽△ACB.
(2)解:
∵△ADE∽△ACB,
∴∠ADE=∠C,
∵AF平分∠BAC,
∴∠DAG=∠CAF,
∴△ADG∽△ACF,
∴$\frac{AG}{AF}=\frac{AD}{AC}$,
∵AD=2,AC=3,
∴$\frac{AG}{AF}=\frac{2}{3}$,
∴$\frac{AG}{GF}=2$.
查看更多完整答案,请扫码查看


