《2025年名师面对面学科素养评价九年级数学全一册浙教版》

7. 如图，$\angle APD=90^{\circ}$，$AP=PB=BC=CD$，则下列结论成立的是 (B)

A.$\triangle PAB\backsim\triangle PCA$
B.$\triangle ABC\backsim\triangle DBA$
C.$\triangle PAB\backsim\triangle PDA$
D.$\triangle ABC\backsim\triangle DCA$
]

答案： 7.B

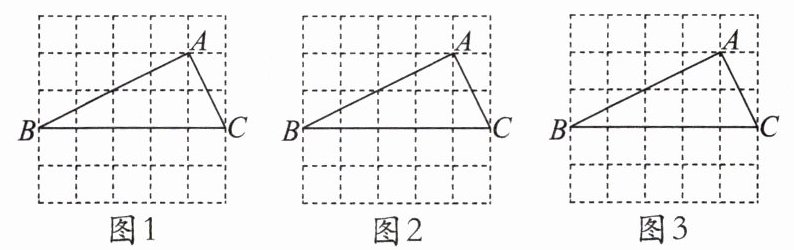
8. 图 1、图 2、图 3 均是$5×5$的正方形网格，每个小正方形的边长均为$1$，其顶点称为格点，$\triangle ABC$的顶点均在格点上.只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹.
(1) 网格中$\triangle ABC$的形状是直角三角形.
(2) 在图 1 中确定一点$D$，连结$DB$，$DC$，使$\triangle DBC$与$\triangle ABC$全等.
(3) 在图 2 中$\triangle ABC$的边$BC$上确定一点$E$，连结$AE$，使$\triangle ABE\backsim\triangle CBA$.
(4) 在图 3 中$\triangle ABC$的边$AB$上确定一点$P$，在边$BC$上确定一点$Q$，连结$PQ$，使$\triangle PBQ\backsim\triangle ABC$，且相似比为$1:2$.
]

答案：
8.解:
(1)直角三角形。
(2)如图1中，点D，点D'，点D"即为所求。
(3)如图2中，点E即为所求。
(4)如图3，点P，点Q即为所求。
　　

9. 如图，在正方形$ABCD$中，点$E$在边$BC$上，连结$AE$，$\angle DAE$的平分线$AG$与边$CD$交于点$G$，与$BC$的延长线交于点$F$.设$\frac{CE}{EB}=\lambda(\lambda＞0)$.
(1) 若$AB=2$，$\lambda=1$，求线段$CF$的长.
(2) 连结$EG$，若$EG\perp AF$，
① 求证：$G$为边$CD$的中点.
② 求$\lambda$的值.
]

答案： 9.解:
(1)可证EF=AE=$\sqrt{AB^{2}+BE^{2}}=\sqrt{5}$，CF=EF−EC =$\sqrt{5}$−1。
(2)①证明:可证△ADG≌△FCG(AAS)，
∴DG=CG，即点G为CD的中点；
　②设CD=2a，则CG=a，由①知，CF=DA=2a，
　可证△EGC∽△GFC，
∴$\frac{EC}{GC}$=$\frac{GC}{FC}$，
∵GC=a，FC=2a，
∴$\frac{GC}{FC}$=$\frac{1}{2}$，
∴$\frac{EC}{GC}$=$\frac{1}{2}$，
∴EC=$\frac{1}{2}$a，
BE=BC−EC=2a−$\frac{1}{2}$a=$\frac{3}{2}$a，
∴λ=$\frac{CE}{EB}$=$\frac{\frac{1}{2}a}{\frac{3}{2}a}$=$\frac{1}{3}$。