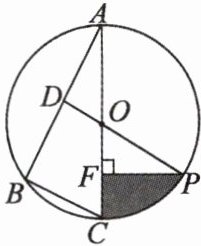
【例 2】如图,已知 $\odot O$ 是 $\triangle ABC$ 的外接圆,$AC$ 是直径,$\angle A = 30°$,$BC = 2$,$D$ 是 $AB$ 的中点。连结 $DO$ 并延长交 $\odot O$ 于点 $P$,过点 $P$ 作 $PF\perp AC$ 于点 $F$。
(1) 求劣弧 $PC$ 的长。(结果保留 $\pi$)
(2) 求阴影部分的面积。(结果保留 $\pi$)
(1) 求劣弧 $PC$ 的长。(结果保留 $\pi$)
(2) 求阴影部分的面积。(结果保留 $\pi$)

答案:
(1)
∵∠A=30°,
∴在Rt△ABC中,
OA=BC=2,∠POF=60°,
∴⊙O的半径为2,
∴劣弧PC的长$l$=$\frac{nπr}{180}$=$\frac{60π×2}{180}$=$\frac{2}{3}$π.
(2)
∵OF=$\frac{1}{2}$OP,
∴OF=1,
∴PF=$\sqrt{OP²−OF²}$=$\sqrt{3}$,
∴$S_{阴影}$=$S_{扇形}$−$S_{\triangle OPF}$=$\frac{60π×2^{2}}{360}$−$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{2}{3}$π−$\frac{\sqrt{3}}{2}$.
(1)
∵∠A=30°,
∴在Rt△ABC中,
OA=BC=2,∠POF=60°,
∴⊙O的半径为2,
∴劣弧PC的长$l$=$\frac{nπr}{180}$=$\frac{60π×2}{180}$=$\frac{2}{3}$π.
(2)
∵OF=$\frac{1}{2}$OP,
∴OF=1,
∴PF=$\sqrt{OP²−OF²}$=$\sqrt{3}$,
∴$S_{阴影}$=$S_{扇形}$−$S_{\triangle OPF}$=$\frac{60π×2^{2}}{360}$−$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{2}{3}$π−$\frac{\sqrt{3}}{2}$.
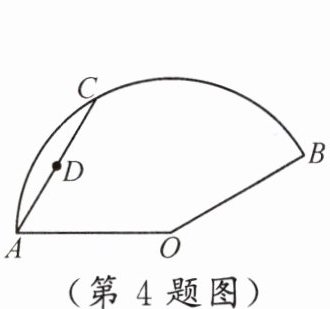
练习 4 如图,扇形 $AOB$ 中,$\angle AOB = 150°$,$AC = AO = 6$,$D$ 为 $AC$ 的中点。当弦 $AC$ 沿扇形运动时,点 $D$ 所经过的路程为 (
A.$3\pi$
B.$\sqrt{3}\pi$
C.$\frac{3\sqrt{3}}{2}\pi$
D.$4\pi$
C
)
A.$3\pi$
B.$\sqrt{3}\pi$
C.$\frac{3\sqrt{3}}{2}\pi$
D.$4\pi$
答案:
练习4.C
练习 5 如图,一根 $5$ 米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊 $A$(羊在草地上活动),那么羊在草地上的最大活动区域面积是 (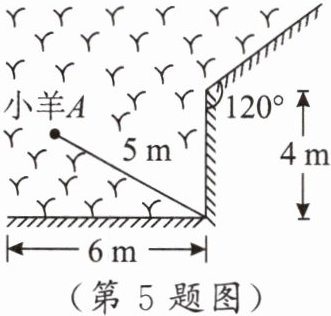
A.$\frac{17}{12}\pi$ 平方米
B.$\frac{17}{6}\pi$ 平方米
C.$\frac{25}{4}\pi$ 平方米
D.$\frac{77}{12}\pi$ 平方米
D
)
A.$\frac{17}{12}\pi$ 平方米
B.$\frac{17}{6}\pi$ 平方米
C.$\frac{25}{4}\pi$ 平方米
D.$\frac{77}{12}\pi$ 平方米
答案:
练习5.D
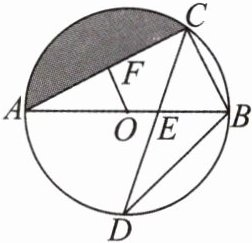
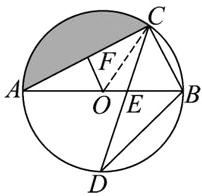
练习 6 如图,$AB$ 是 $\odot O$ 的直径,弦 $CD$ 交 $AB$ 于点 $E$,$OF\perp AC$ 于点 $F$。
(1) 请探索 $OF$ 和 $BC$ 的关系并说明理由。
(2) 若 $\angle D = 30°$,$BC = 1$,求圆中阴影部分的面积。(结果保留 $\pi$)
(1) 请探索 $OF$ 和 $BC$ 的关系并说明理由。
(2) 若 $\angle D = 30°$,$BC = 1$,求圆中阴影部分的面积。(结果保留 $\pi$)

答案:
(1)OF//BC,OF=$\frac{1}{2}$BC.
理由:由垂径定理得AF=CF.
∵AO=BO,
∴OF是△ABC的中位线.
∴OF//BC,OF=$\frac{1}{2}$BC.
(2)连结OC.由
(1)知OF=$\frac{1}{2}$.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠D=30°,
∴∠A=30°.
∴AB=2BC=2.
∴AC=$\sqrt{3}$
∴$S_{\triangle AOC}$=$\frac{1}{2}$×AC×OF=$\frac{\sqrt{3}}{4}$.
∵∠AOC=120°,OA=1,
∴$S_{扇形AOC}$=$\frac{120 \cdot \pi \cdot OA^{2}}{360}$=$\frac{π}{3}$.
∴$S_{阴影}$=$S_{扇形AOC}$−$S_{\triangle AOC}$=$\frac{π}{3}$−$\frac{\sqrt{3}}{4}$.
(1)OF//BC,OF=$\frac{1}{2}$BC.
理由:由垂径定理得AF=CF.
∵AO=BO,
∴OF是△ABC的中位线.
∴OF//BC,OF=$\frac{1}{2}$BC.

(2)连结OC.由
(1)知OF=$\frac{1}{2}$.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵∠D=30°,
∴∠A=30°.
∴AB=2BC=2.
∴AC=$\sqrt{3}$
∴$S_{\triangle AOC}$=$\frac{1}{2}$×AC×OF=$\frac{\sqrt{3}}{4}$.
∵∠AOC=120°,OA=1,
∴$S_{扇形AOC}$=$\frac{120 \cdot \pi \cdot OA^{2}}{360}$=$\frac{π}{3}$.
∴$S_{阴影}$=$S_{扇形AOC}$−$S_{\triangle AOC}$=$\frac{π}{3}$−$\frac{\sqrt{3}}{4}$.
查看更多完整答案,请扫码查看


