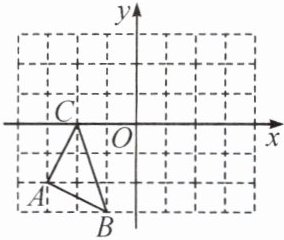
7. 如图,$\triangle ABC$的三个顶点$A(-3,-2)$,$B(-1,-3)$,$C(-2,0)$.以原点$O$为位似中心,将$\triangle ABC$缩小,使变换后得到$\triangle DEF$与$\triangle ABC$的位似比为$1:2$,那么顶点$A$的对应点$D$的坐标为(
A.$(-1,-1)$
B.$(-1,-1)$或$(1,1)$
C.$(1,-1)$
D.$(-\frac{3}{2},-1)$或$(\frac{3}{2},1)$
D
)
A.$(-1,-1)$
B.$(-1,-1)$或$(1,1)$
C.$(1,-1)$
D.$(-\frac{3}{2},-1)$或$(\frac{3}{2},1)$
答案:
7.D
8. 如图,已知$B'C'// BC$,$C'D'// CD$,$D'E'// DE$.
(1) 求证:四边形$BCDE$与四边形$B'C'D'E'$相似.
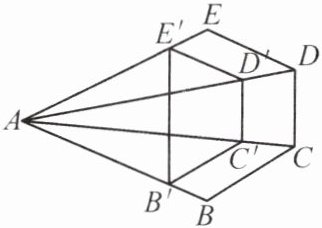
(2) 若$\frac{AB'}{BB'}=3$,$S_{四边形BCDE}=20$,求$S_{四边形B'C'D'E'}$.
(1) 求证:四边形$BCDE$与四边形$B'C'D'E'$相似.

(2) 若$\frac{AB'}{BB'}=3$,$S_{四边形BCDE}=20$,求$S_{四边形B'C'D'E'}$.
答案:
8.解:
(1)证明:
∵B'C'//BC,C'D'//CD,D'E'//DE,
∴$\frac{AD'}{AD}=\frac{AC'}{AC}=\frac{C'D'}{CD}=\frac{E'D'}{ED}=\frac{B'C'}{BC}=\frac{B'E'}{BE}$。
又四边形BCDE与四边形B'C'D'E'对应顶点的连线相交于一点A,
∴四边形BCDE位似于四边形B'C'D'E'
(2)
∵$\frac{AB'}{BB'}$=3,
∴$\frac{AB'}{AB}$=$\frac{3}{4}$,
∴四边形BCDE与四边形B'C'D'E'位似比为$\frac{4}{3}$,又
∵S四边形BCDE=20,
∴S四边形B'C'D'E'=$\frac{20}{(\frac{4}{3})^2}$=$\frac{45}{4}$。
(1)证明:
∵B'C'//BC,C'D'//CD,D'E'//DE,
∴$\frac{AD'}{AD}=\frac{AC'}{AC}=\frac{C'D'}{CD}=\frac{E'D'}{ED}=\frac{B'C'}{BC}=\frac{B'E'}{BE}$。
又四边形BCDE与四边形B'C'D'E'对应顶点的连线相交于一点A,
∴四边形BCDE位似于四边形B'C'D'E'
(2)
∵$\frac{AB'}{BB'}$=3,
∴$\frac{AB'}{AB}$=$\frac{3}{4}$,
∴四边形BCDE与四边形B'C'D'E'位似比为$\frac{4}{3}$,又
∵S四边形BCDE=20,
∴S四边形B'C'D'E'=$\frac{20}{(\frac{4}{3})^2}$=$\frac{45}{4}$。
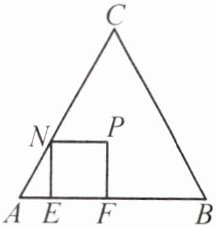
9. 如图,等边三角形$ABC$的边长为$3+\sqrt{3}$.
(1) 如图,正方形$EFPN$的顶点$E$,$F$在边$AB$上,顶点$N$在边$AC$上,在等边三角形$ABC$及其内部,以点$A$为位似中心,作正方形$EFPN$的位似正方形$E'F'P'N'$,且使正方形$E'F'P'N'$的面积最大.(不要求写作法)
(2) 求(1)中作出的正方形$E'F'P'N'$的边长.
(1) 如图,正方形$EFPN$的顶点$E$,$F$在边$AB$上,顶点$N$在边$AC$上,在等边三角形$ABC$及其内部,以点$A$为位似中心,作正方形$EFPN$的位似正方形$E'F'P'N'$,且使正方形$E'F'P'N'$的面积最大.(不要求写作法)
(2) 求(1)中作出的正方形$E'F'P'N'$的边长.

答案:
9.解:
(1)如图,正方形E'F'P'N'即为所求.
(2)设正方形E'F'P'N'的边长为x,
∵△ABC为正三角形,
∴AE'=BF'=$\frac{\sqrt{3}}{3}$x。
∵E'F'+AE'+BF'=AB,
∴x+$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$x=3+$\sqrt{3}$,
∴x=$\frac{9+3\sqrt{3}}{2\sqrt{3}+3}$,
即x=3$\sqrt{3}$−3。

9.解:
(1)如图,正方形E'F'P'N'即为所求.
(2)设正方形E'F'P'N'的边长为x,
∵△ABC为正三角形,
∴AE'=BF'=$\frac{\sqrt{3}}{3}$x。
∵E'F'+AE'+BF'=AB,
∴x+$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$x=3+$\sqrt{3}$,
∴x=$\frac{9+3\sqrt{3}}{2\sqrt{3}+3}$,
即x=3$\sqrt{3}$−3。

查看更多完整答案,请扫码查看


