《2025年名师面对面学科素养评价九年级数学全一册浙教版》

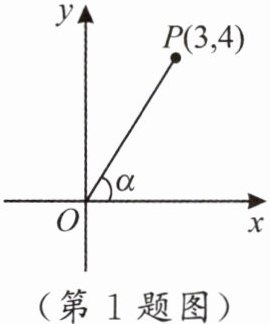
1. 如图，在平面直角坐标系内有一点 $ P(3,4) $，连结 $ OP $，设 $ OP $ 与 $ x $ 轴正半轴所夹的锐角为 $ \alpha $，则锐角 $ \alpha $ 的正弦值为(B)

A.$ \frac{3}{5} $
B.$ \frac{4}{5} $
C.$ \frac{3}{4} $
D.$ \frac{4}{3} $

答案： 1.B

2. 在 $ Rt\triangle ABC $ 中，若各边长度都扩大到原来的 $ 3 $ 倍，则锐角 $ A $ 的各个三角函数值(A)

A.不变化
B.扩大到原来的 $ 3 $ 倍
C.缩小到原来的 $ \frac{1}{3} $
D.缩小到原来的 $ \frac{1}{9} $

答案： 2.A

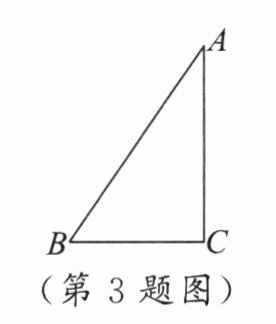
3. 如图，在 $ Rt\triangle ABC $ 中，$ \angle C = 90^{\circ} $。若 $ AB = 5 $，$ AC = 4 $，则 $ \tan B = $(D)

A.$ \frac{3}{5} $
B.$ \frac{4}{5} $
C.$ \frac{3}{4} $
D.$ \frac{4}{3} $

答案： 3.D

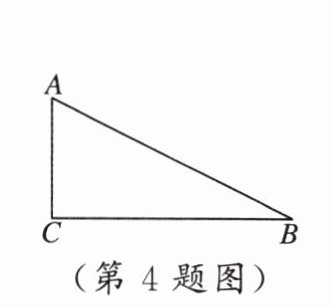
4. 如图，在 $ \triangle ABC $ 中，$ \angle C = 90^{\circ} $，设 $ \angle A $，$ \angle B $，$ \angle C $ 所对的边分别为 $ a $，$ b $，$ c $，则(B)

A.$ c = b\sin B $
B.$ b = c\sin B $
C.$ a = b\tan B $
D.$ b = c\tan B $

答案： 4.B

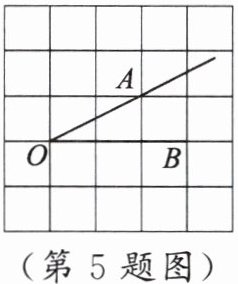
5. 如图，将 $ \angle AOB $ 放在边长为 $ 1 $ 的小正方形组成的网格中，则 $ \tan \angle AOB = $$\frac{1}{2}$。

答案： 5.$\frac{1}{2}$

6. 如图，在 $ \triangle ABC $ 中，$ \angle ABC = 90^{\circ} $，$ BD \perp AC $ 于点 $ D $，$ \angle CBD = \alpha $，$ AB = 3 $，$ BC = 4 $。求 $ \sin \alpha $，$ \cos \alpha $，$ \tan \alpha $ 的值。
]

答案： 6.解:
∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵BD⊥AC,
∴∠A+∠ABD=90°,
∴∠A=∠CBD=α,
∵∠ABC=90°,AB=3,BC=4,
∴AC=5,
　sinα=sin∠A=$\frac{BC}{AC}$=$\frac{4}{5}$,cosα=$\frac{3}{5}$,tanα=$\frac{4}{3}$.