《2025年名师面对面学科素养评价九年级数学全一册浙教版》

【例 1】已知抛物线 $ y = ax^{2} - 2ax - 8(a \neq 0) $ 经过点 $ (-2,0) $。
(1) 求抛物线的函数表达式和顶点坐标。
(2) 直线 $ l $ 交抛物线于点 $ A(-4,m) $，$ B(n,7) $，$ n $ 为正数。若点 $ P $ 在抛物线上且在直线 $ l $ 下方（不与点 $ A $，$ B $ 重合），分别求出点 $ P $ 横坐标与纵坐标的取值范围。

答案：
(1)函数表达式为$y = x^{2} - 2x - 8$，顶点坐标为$(1,-9)$。
(2)由题意，得$m = 16$，$n = 5$，
$\therefore$点A坐标为$(-4,16)$，点B坐标为$(5,7)$。
$\because$抛物线开口向上，顶点坐标为$(1,-9)$，
$\therefore$抛物线顶点在AB下方，$\therefore - 4 ＜ x_{P} ＜ 5$，$-9 \leq y_{P} ＜ 16$。

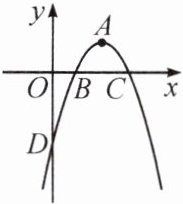
【例 2】如图，在平面直角坐标系中，二次函数 $ y = ax^{2} + 4x - 3 $ 图象的顶点是 $ A $，与 $ x $ 轴交于 $ B $，$ C $ 两点，与 $ y $ 轴交于点 $ D $，点 $ B $ 的坐标是 $ (1,0) $。
(1) 求 $ A $，$ C $ 两点的坐标，并根据图象直接写出当 $ y ＞ 0 $ 时 $ x $ 的取值范围。
(2) 平移该二次函数的图象，使点 $ D $ 恰好落在点 $ A $ 的位置上，求平移后图象所对应的二次函数的表达式。

答案：
(1)$A(2,1)$，$C(3,0)$，当$y ＞ 0$时，$1 ＜ x ＜ 3$。
(2)$\because D(0,-3)$，$\therefore$点D平移到点A，抛物线向右平移2个单位，向上平移4个单位，可得抛物线的解析式为$y = -(x - 4)^{2} + 5$。

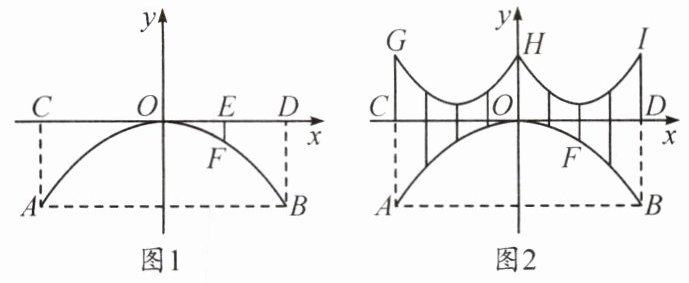
【例 3】图 1 是一座抛物线型拱桥侧面示意图。水面宽 $ AB $ 与桥长 $ CD $ 均为 $ 24m $，在距离 $ D $ 点 $ 6m $ 的 $ E $ 处，测得桥面到桥拱的距离 $ EF $ 为 $ 1.5m $，以桥拱顶点 $ O $ 为原点，桥面为 $ x $ 轴建立平面直角坐标系。
(1) 求桥拱顶部 $ O $ 离水面的距离。
(2) 如图 2，桥面上方有 $ 3 $ 根高度均为 $ 4m $ 的支柱 $ CG $，$ OH $，$ DI $，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为 $ 1m $。
① 求出其中一条钢缆抛物线的函数表达式。
② 为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值。

答案：
(1)根据题意可求出拱桥侧面所在抛物线的函数表达式为$y_{1} = -\frac{1}{24}x^{2}$，当$x = 12$时，$y_{1} = -\frac{1}{24} × 12^{2} = -6$，
$\therefore$桥拱顶部离水面高度为$6m$。
(2)①可设右边钢缆所在抛物线的函数表达式为$y_{2} = a_{2}(x - 6)^{2} + 1$，将$H(0,4)$代入，求得$a_{2} = \frac{1}{12}$，
$\therefore$右边钢缆所在抛物线的函数表达式为$y_{2} = \frac{1}{12}(x - 6)^{2} + 1$，同理可得左边钢缆所在抛物线的函数表达式为$y_{3} = \frac{1}{12}(x + 6)^{2} + 1$；
②设彩带的长度为$Lm$，
则$L = y_{2} - y_{1} = \frac{1}{12}(x - 6)^{2} + 1 - (-\frac{1}{24}x^{2}) = \frac{1}{8}x^{2} - x + 4 = \frac{1}{8}(x - 4)^{2} + 2$，$\therefore$当$x = 4$时，$L$最小值$= 2$，
答：彩带长度的最小值是$2m$。