7. 《千里江山图》是宋代王希孟的作品. 如图,它的局部画面装裱前是一个长为 $2.4$ 米,宽为 $1.4$ 米的矩形,装裱后,整幅图画宽与长的比是 $8:13$,且四周边衬的宽度相等,则边衬的宽度应是多少米?设边衬的宽度为 $x$ 米,根据题意可列方程(

A.$\frac{1.4 - x}{2.4 - x} = \frac{8}{13}$
B.$\frac{1.4 + x}{2.4 + x} = \frac{8}{13}$
C.$\frac{1.4x - 2x}{2.4 - 2x} = \frac{8}{13}$
D.$\frac{1.4 + 2x}{2.4 + 2x} = \frac{8}{13}$
D
)
A.$\frac{1.4 - x}{2.4 - x} = \frac{8}{13}$
B.$\frac{1.4 + x}{2.4 + x} = \frac{8}{13}$
C.$\frac{1.4x - 2x}{2.4 - 2x} = \frac{8}{13}$
D.$\frac{1.4 + 2x}{2.4 + 2x} = \frac{8}{13}$
答案:
7.D
8. 已知三条线段的长度分别为 $a$,$b$,$c$. 若$\frac{a + b}{c} = \frac{a + c}{b} = \frac{b + c}{a} = k$,则 $k$ 的值是
2
.
答案:
8.2
9. 已知 $a$,$b$,$c$ 是$\triangle ABC$ 的三边长,且$\frac{a}{5} = \frac{b}{4} = \frac{c}{6} \neq 0$. 求:
(1) $\frac{2a + b}{3c}$的值.
(2) 若$\triangle ABC$ 的周长为 $90$,求各边的长.
(1) $\frac{2a + b}{3c}$的值.
(2) 若$\triangle ABC$ 的周长为 $90$,求各边的长.
答案:
9.解:设$\frac{a}{5}=\frac{b}{4}=\frac{c}{6}=m\neq0$,则$a = 5m$,$b = 4m$,$c = 6m$.
(1)$\frac{2a + b}{3c}=\frac{2×5m + 4m}{3×6m}=\frac{14}{18}=\frac{7}{9}$.
(2)$a + b + c = 5m + 4m + 6m = 90$,可得$m = 6$,
∴$a = 30$,$b = 24$,$c = 36$.
(1)$\frac{2a + b}{3c}=\frac{2×5m + 4m}{3×6m}=\frac{14}{18}=\frac{7}{9}$.
(2)$a + b + c = 5m + 4m + 6m = 90$,可得$m = 6$,
∴$a = 30$,$b = 24$,$c = 36$.
10. 如图所示,在$□ ABCD$ 中,$DE \perp AB$ 于点 $E$,$BF \perp AD$ 于点 $F$.
(1) $AB$,$BC$,$BF$,$DE$ 这四条线段能否成比例?若不能,请说明理由;若能,请写出比例式.
(2) 若 $AB = 10$,$DE = 2.5$,$BF = 5$,求 $BC$ 的长.
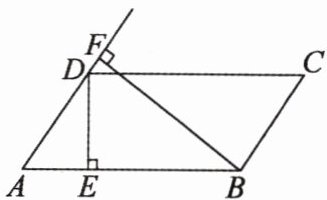
(1) $AB$,$BC$,$BF$,$DE$ 这四条线段能否成比例?若不能,请说明理由;若能,请写出比例式.
(2) 若 $AB = 10$,$DE = 2.5$,$BF = 5$,求 $BC$ 的长.

答案:
10.解:
(1)
∵在$□ ABCD$中,$DE⊥AB$,$BF⊥AD$,
∴$S_{□ ABCD}=AB×DE = AD×BF$,
∴$\frac{AD}{DE}=\frac{AB}{BF}$,即$\frac{BC}{DE}=\frac{AB}{BF}$.
(2)
∵$AB·DE = AD·BF$,
∴$10×2.5 = 5BC$,解得$BC = 5$.
(1)
∵在$□ ABCD$中,$DE⊥AB$,$BF⊥AD$,
∴$S_{□ ABCD}=AB×DE = AD×BF$,
∴$\frac{AD}{DE}=\frac{AB}{BF}$,即$\frac{BC}{DE}=\frac{AB}{BF}$.
(2)
∵$AB·DE = AD·BF$,
∴$10×2.5 = 5BC$,解得$BC = 5$.
查看更多完整答案,请扫码查看


