一、锐角三角函数的概念
【例 1】在锐角△ABC 中,AB = 15,BC = 14,$S_{△ABC} = 84,$则 tan C 的值为
【例 1】在锐角△ABC 中,AB = 15,BC = 14,$S_{△ABC} = 84,$则 tan C 的值为
$\frac{12}{5}$
。
答案:
【例1】$\frac{12}{5}$
练习 1 计算:
(1) 2sin 60° + cos 45° - tan 60°。
(2) √3 sin 60° + tan 60° - 2cos²30°。
(1) 2sin 60° + cos 45° - tan 60°。
(2) √3 sin 60° + tan 60° - 2cos²30°。
答案:
练习1.解:
(1)原式$=2 × \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} - \sqrt{3} = \sqrt{3} + \frac{\sqrt{2}}{2} - \sqrt{3} = \frac{\sqrt{2}}{2}$.
(2)原式$=\sqrt{3} × \frac{\sqrt{3}}{2} + \sqrt{3} - 2 × (\frac{\sqrt{3}}{2})^2 = \frac{3}{2} + \sqrt{3} - \frac{3}{2} = \sqrt{3}$.
(1)原式$=2 × \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} - \sqrt{3} = \sqrt{3} + \frac{\sqrt{2}}{2} - \sqrt{3} = \frac{\sqrt{2}}{2}$.
(2)原式$=\sqrt{3} × \frac{\sqrt{3}}{2} + \sqrt{3} - 2 × (\frac{\sqrt{3}}{2})^2 = \frac{3}{2} + \sqrt{3} - \frac{3}{2} = \sqrt{3}$.
【例 2】如图,在四边形 ABCD 中,∠ABC = 90°,∠ADC = 90°,AB = 6,CD = 4,BC 的延长线与 AD 的延长线交于点 E。(注意:本题中的计算过程和结果均保留根号)
(1) 若∠A = 60°,求 BC 的长。
(2) 若 sin A = $\frac{4}{5}$,求 AD 的长。
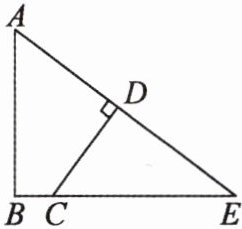
(1) 若∠A = 60°,求 BC 的长。
(2) 若 sin A = $\frac{4}{5}$,求 AD 的长。

答案:
【例2】解:
(1)$\because \angle A = 60^{\circ}$,$\angle ABE = 90^{\circ}$,$AB = 6$,$\tan A = \frac{BE}{AB}$,
$\therefore \angle E = 30^{\circ}$,$BE = \tan 60^{\circ} \cdot 6 = 6\sqrt{3}$,又$\because \angle CDE = 90^{\circ}$,$CD = 4$,$CE = 8$,$\therefore BC = BE - CE = 6\sqrt{3} - 8$.
(2)$\because \angle ABE = 90^{\circ}$,$AB = 6$,由$\sin A = \frac{4}{5}$,
得$\tan A = \frac{4}{3}$,即$\frac{BE}{AB} = \frac{4}{3}$,又$\because \triangle ABE \backsim \triangle CDE$,
$\therefore \frac{DE}{CD} = \frac{BE}{AB} = \frac{4}{3}$,解得$DE = \frac{16}{3}$,
$\therefore AD = AE - DE = 10 - \frac{16}{3} = \frac{14}{3}$,即$AD$的长是$\frac{14}{3}$.
(1)$\because \angle A = 60^{\circ}$,$\angle ABE = 90^{\circ}$,$AB = 6$,$\tan A = \frac{BE}{AB}$,
$\therefore \angle E = 30^{\circ}$,$BE = \tan 60^{\circ} \cdot 6 = 6\sqrt{3}$,又$\because \angle CDE = 90^{\circ}$,$CD = 4$,$CE = 8$,$\therefore BC = BE - CE = 6\sqrt{3} - 8$.
(2)$\because \angle ABE = 90^{\circ}$,$AB = 6$,由$\sin A = \frac{4}{5}$,
得$\tan A = \frac{4}{3}$,即$\frac{BE}{AB} = \frac{4}{3}$,又$\because \triangle ABE \backsim \triangle CDE$,
$\therefore \frac{DE}{CD} = \frac{BE}{AB} = \frac{4}{3}$,解得$DE = \frac{16}{3}$,
$\therefore AD = AE - DE = 10 - \frac{16}{3} = \frac{14}{3}$,即$AD$的长是$\frac{14}{3}$.
练习 2 如图,在 Rt△ABC 中,∠ACB = 90°,AC = 4,tan A = $\frac{3}{4}$。以点 C 为圆心、CB 长为半径的圆交 AB 于点 D,则 AD 的长是 (
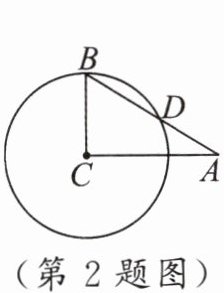
A.1
B.$\frac{7}{5}$
C.$\frac{3}{2}$
D.2
B
)
A.1
B.$\frac{7}{5}$
C.$\frac{3}{2}$
D.2
答案:
练习2.B
练习 3 如图所示,在四边形 ABCD 中,∠B = 90°,AB = 2,CD = 8。连结 AC,AC ⊥ CD。若 sin∠ACB = $\frac{1}{3}$,则 AD 的长是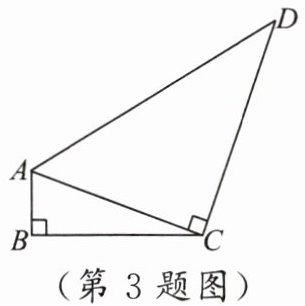
10
。
答案:
练习3.10
查看更多完整答案,请扫码查看


