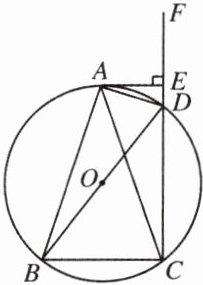
【例 1】如
(1) 求证:$AB = AC$。
(2) 若 $BD = 11$,$DE = 2$,求 $CD$ 的长。
图
,四边形 $ABCD$ 是 $\odot O$ 的内接四边形,$F$ 是 $CD$ 延长线上的一点,且 $AD$ 平分 $\angle BDF$,$AE\perp CD$ 于点 $E$。(1) 求证:$AB = AC$。
(2) 若 $BD = 11$,$DE = 2$,求 $CD$ 的长。

答案:
(1)证明:
∵AD平分∠BDF,
∴∠ADF=∠ADB,
∵∠ADF=∠ABC,∠ACB=∠ADB,
∴∠ABC=∠ACB,
∴AB=AC.

(2)解:过点A作AG⊥BD,垂足为点G.可证
Rt△AED≌Rt△AGD,
∴GD=ED=2,
在Rt△AEC和Rt△AGB中,$\begin{cases}AE = AG, \\AB = AC,\end{cases}$
∴Rt△AEC≌Rt△AGB(HL),
∴BG=CE,
∵BD=11,
∴BG=BD−GD=11−2=9,
∴CE=BG=9,
∴CD=CE−DE=9−2=7.
(1)证明:
∵AD平分∠BDF,
∴∠ADF=∠ADB,
∵∠ADF=∠ABC,∠ACB=∠ADB,
∴∠ABC=∠ACB,
∴AB=AC.

(2)解:过点A作AG⊥BD,垂足为点G.可证
Rt△AED≌Rt△AGD,
∴GD=ED=2,
在Rt△AEC和Rt△AGB中,$\begin{cases}AE = AG, \\AB = AC,\end{cases}$
∴Rt△AEC≌Rt△AGB(HL),
∴BG=CE,
∵BD=11,
∴BG=BD−GD=11−2=9,
∴CE=BG=9,
∴CD=CE−DE=9−2=7.
练习 1 如图,四边形 $ABCD$ 内接于 $\odot O$,$AE\perp CB$ 交 $CB$ 的延长线于点 $E$。若 $BA$ 平分 $\angle DBE$,$AD = 5$,$CE = \sqrt{13}$,则 $AE =$ (
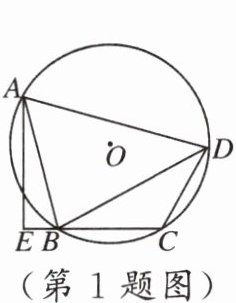
A.$3$
B.$3\sqrt{2}$
C.$4\sqrt{3}$
D.$2\sqrt{3}$
D
)
A.$3$
B.$3\sqrt{2}$
C.$4\sqrt{3}$
D.$2\sqrt{3}$
答案:
练习1.D
练习 2 如图,在 $\triangle ABC$ 中,$\angle ACB = 90°$,过 $B$,$C$ 两点的 $\odot O$ 交 $AC$ 于点 $D$,交 $AB$ 于点 $E$,连结 $EO$ 并延长交 $\odot O$ 于点 $F$,连结 $BF$,$CF$。若 $\angle EDC = 135°$,$CF = 2\sqrt{2}$,则 $AE^2 + BE^2$ 的值为 (
A.$8$
B.$12$
C.$16$
D.$20$
C
)
A.$8$
B.$12$
C.$16$
D.$20$
答案:
练习2.C [解析]可证△ACE≌△BCF(ASA),
∴AE=BF,
∵Rt△ECF中,CF=2$\sqrt{2}$,∠EFC=45°,
∴EF²=16,
则AE²+BE²=BF²+BE²=EF²=16.
∴AE=BF,
∵Rt△ECF中,CF=2$\sqrt{2}$,∠EFC=45°,
∴EF²=16,
则AE²+BE²=BF²+BE²=EF²=16.
练习 3 如图,五边形 $ABCDE$ 是 $\odot O$ 的内接正五边形,$AF$ 是 $\odot O$ 的直径,则 $\angle BDF$ 的度数是  $°$。
$°$。
54
 $°$。
$°$。
答案:
练习3.54
查看更多完整答案,请扫码查看


