《2025年名师面对面学科素养评价九年级数学全一册浙教版》

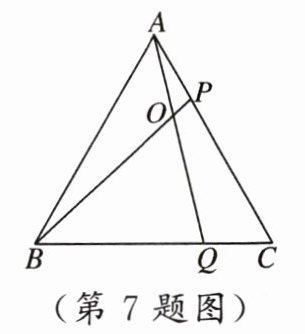
7. 如图，在等边三角形$ABC$的边$AC$，$BC$上各取一点$P$，$Q$，使$AP = CQ$，$AQ$，$BP$相交于点$O$。若$BO = 6$，$PO = 2$，则$AP$的长为4。
]

答案： 7.4

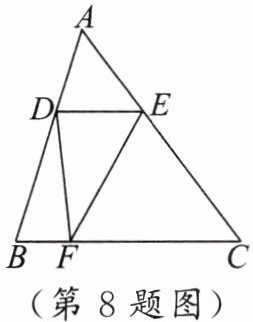
8. 如图，$D$，$E$，$F$分别是$\triangle ABC$三边上的点，其中$BC = 8$，$BC$边上的高为$6$，且$DE // BC$，则$\triangle DEF$面积的最大值为(A)

A.$6$
B.$8$
C.$10$
D.$12$

答案： 8.A【解析】设DE=x，由相似求出△DEF的高，列出表示△DEF的面积的函数表达式，由函数的性质得出最大值.

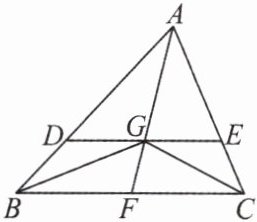
9. 如图，过$\triangle ABC$的重心$G$作$BC$的平行线分别交$AB$，$AC$于点$D$，$E$，求$\frac{S_{\triangle GBC}}{S_{\triangle ADE}}$的值。

]

答案： 9.解：令△ADE中DE边上的高为$h_1$，△GBC中BC边上的高为$h_2$.
∵G是△ABC的重心，DE//BC，
∴△ADG∽△ABF，
∴$\frac{DG}{BF}=\frac{h_1}{h_1+h_2}=\frac{AG}{AF}=\frac{2}{3}$，
同理$\frac{GE}{FC}=\frac{2}{3}$，
∴$\frac{S_{\triangle GBC}}{S_{\triangle ADE}}=\frac{\frac{1}{2}h_2\cdot BC}{\frac{1}{2}h_1\cdot DE}=\frac{3}{4}$.

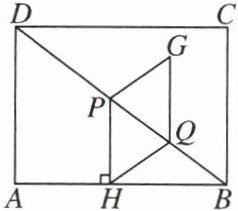
10. 如图，在矩形$ABCD$中，$AB = 4$，$BC = 3$，点$P$，$Q$在对角线$BD$上，且$BQ = \frac{2}{3}BP$。过点$P$作$PH \perp AB$于点$H$，连结$HQ$，以$PH$，$HQ$为邻边作平行四边形$PHQG$，设$BQ = m$。
(1) 若$m = 2$，求$PH$的长。
(2) 若点$C$，$G$，$H$在同一直线上，求$m$的值。

]

答案：
10.解：
(1)在矩形ABCD中，AB=4，BC=3，
∴$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{16+9}=5$，

∵BQ=2，$BQ=\frac{2}{3}BP$，
∴BP=3，
∵PH//AD，
∴△BPH∽△BDA，
∴$\frac{PH}{AD}=\frac{BP}{BD}$，
∴$PH=\frac{AD\cdot BP}{BD}=\frac{9}{5}$.
(2)如图，设HG与PQ交于点O，
设BQ=2x，则BP=3x，PQ=x，
∴$PO=QO=\frac{1}{2}x$，
∴$BO=\frac{5}{2}x$，
∵PH//BC，
∴△PHO∽△BCO，
∴$\frac{PH}{BC}=\frac{PO}{OB}$，
∴$PH=\frac{BC\cdot PO}{OB}=\frac{3}{5}$，
∵PH//AD，
∴△BPH∽△BDA，
∴$\frac{PH}{AD}=\frac{BP}{BD}$，
∵$\frac{\frac{3}{5}}{3}=\frac{3x}{5}$，
∴$x=\frac{1}{3}$，
∴$BQ=m=2x=\frac{2}{3}$.