1. 已知$\triangle ABC$的三边长分别为$6\mathrm{cm}$,$7.5\mathrm{cm}$,$9\mathrm{cm}$,$\triangle DEF$的一边长为$4\mathrm{cm}$,当$\triangle DEF$的另两边长是下列哪一组时,这两个三角形相似 (
A.$2\mathrm{cm}$,$3\mathrm{cm}$
B.$4\mathrm{cm}$,$5\mathrm{cm}$
C.$5\mathrm{cm}$,$6\mathrm{cm}$
D.$6\mathrm{cm}$,$7\mathrm{cm}$
C
)A.$2\mathrm{cm}$,$3\mathrm{cm}$
B.$4\mathrm{cm}$,$5\mathrm{cm}$
C.$5\mathrm{cm}$,$6\mathrm{cm}$
D.$6\mathrm{cm}$,$7\mathrm{cm}$
答案:
1.C
2. 如图,已知$\triangle ABC$和$\triangle PBD$都是正方形网格上的格点三角形(顶点为网格线的交点),要使$\triangle ABC\backsim\triangle PBD$,则点$P$的位置应落在 (
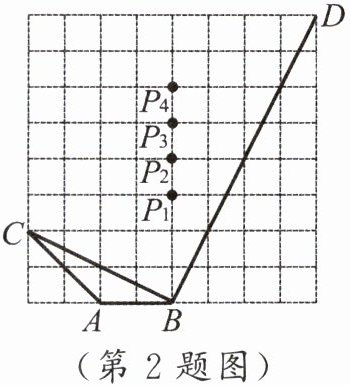
A.点$P_1$上
B.点$P_2$上
C.点$P_3$上
D.点$P_4$上
B
)
A.点$P_1$上
B.点$P_2$上
C.点$P_3$上
D.点$P_4$上
答案:
2.B
3. 如图,小正方形的边长均为$1$,则下列图中的三角形(阴影部分)与$\triangle ABC$相似的是 (
 ]
]
A
) ]
]
答案:
3.A
4. 如图,在$\triangle ABC$中,点$D$在$AB$边上,点$E$在$AC$边上.请添加一个条件,使$\triangle ADE\backsim\triangle ABC$:
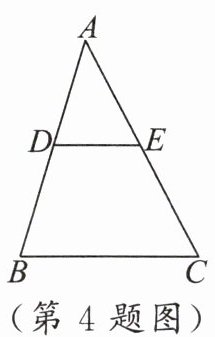
∠ADE=∠B或∠AED=∠C或$\frac{AD}{AB}$=$\frac{AE}{AC}$(答案不唯一)
.
答案:
4.∠ADE=∠B或∠AED=∠C或$\frac{AD}{AB}$=$\frac{AE}{AC}$(答案不唯一)
5. 如图,在$\triangle ABC$中,点$P$在边$AB$上,有下列四个条件:①$\angle ACP=\angle B$;②$\angle APC=\angle ACB$;③$AC^2=AP\cdot AB$;④$AB\cdot CP=AP\cdot CB$.其中能使$\triangle APC$和$\triangle ACB$相似的条件是
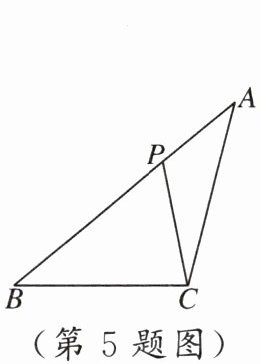
①②③
.(填序号)
答案:
5.①②③
6. 如图,已知$\frac{BD}{BE}=\frac{AD}{CE}=\frac{AB}{BC}$.
求证:$\triangle ABC\backsim\triangle DBE$.
 ]
]
求证:$\triangle ABC\backsim\triangle DBE$.
 ]
]
答案:
6.证明:
∵$\frac{BD}{BE}$=$\frac{AD}{CE}$=$\frac{AB}{BC}$,
∴△ABD∽△CBE,
∴∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,即∠ABC=∠DBE。又
∵$\frac{AB}{BC}$=$\frac{BD}{BE}$,即$\frac{AB}{BD}$=$\frac{BC}{BE}$,
∴△ABC∽△DBE。
∵$\frac{BD}{BE}$=$\frac{AD}{CE}$=$\frac{AB}{BC}$,
∴△ABD∽△CBE,
∴∠ABD=∠CBE,
∴∠ABD+∠DBC=∠CBE+∠DBC,即∠ABC=∠DBE。又
∵$\frac{AB}{BC}$=$\frac{BD}{BE}$,即$\frac{AB}{BD}$=$\frac{BC}{BE}$,
∴△ABC∽△DBE。
查看更多完整答案,请扫码查看


