1. 下列说法错误的是(
A.线段的比就是它们的长度之比
B.只要两条线段的长度采用同一单位,那么两条线段的比与所采用的单位无关
C.求两条线段的比,一定要用同一单位,如果单位不同,应先化成同一单位,再求它们的比
D.两条线段的比与两个数的比一样有正有负
D
)A.线段的比就是它们的长度之比
B.只要两条线段的长度采用同一单位,那么两条线段的比与所采用的单位无关
C.求两条线段的比,一定要用同一单位,如果单位不同,应先化成同一单位,再求它们的比
D.两条线段的比与两个数的比一样有正有负
答案:
1.D
2. 下面四条线段中,不能成比例的是(
A.$a = 3$,$b = 6$,$c = 2$,$d = 4$
B.$a = 1$,$b = \sqrt{2}$,$c = \sqrt{6}$,$d = \sqrt{3}$
C.$a = 4$,$b = 6$,$c = 5$,$d = 10$
D.$a = 2$,$b = \sqrt{5}$,$c = \sqrt{15}$,$d = 2\sqrt{3}$
C
)A.$a = 3$,$b = 6$,$c = 2$,$d = 4$
B.$a = 1$,$b = \sqrt{2}$,$c = \sqrt{6}$,$d = \sqrt{3}$
C.$a = 4$,$b = 6$,$c = 5$,$d = 10$
D.$a = 2$,$b = \sqrt{5}$,$c = \sqrt{15}$,$d = 2\sqrt{3}$
答案:
2.C
3. 在一张比例尺为 $1:4000000$ 的地图上,杭州到嘉兴的图上距离约是 $2cm$,则杭州到嘉兴的实际距离约为
80
km.
答案:
3.80
4. 如图所示,已知 $AB:DB = AC:EC$,$AD = 15cm$,$AB = 40cm$,$AC = 28cm$,则 $CE =$
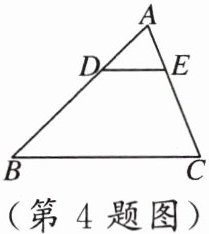
17.5 cm
.
答案:
4.17.5 cm
5. 如图,$\frac{AD}{BD} = \frac{AE}{EC} = \frac{3}{2}$,则$\frac{AB}{BD} =$
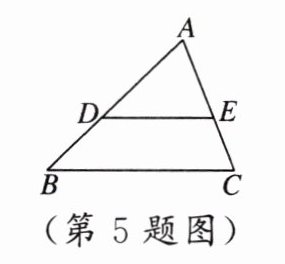
$\frac{5}{2}$
,$\frac{EC}{AC} =$$\frac{2}{5}$
.
答案:
5.$\frac{5}{2}$ $\frac{2}{5}$
6. 已知$\triangle ABC$与$\triangle DEF$在网格中的位置如图所示,每个小正方形的边长都是 $1$.
(1) 求$\frac{AB}{DE}$,$\frac{BC}{EF}$,$\frac{AC}{DF}$的值.
(2) 在 $AB$,$BC$,$AC$,$DE$,$EF$,$DF$ 这六条线段中,找出三组比例线段.
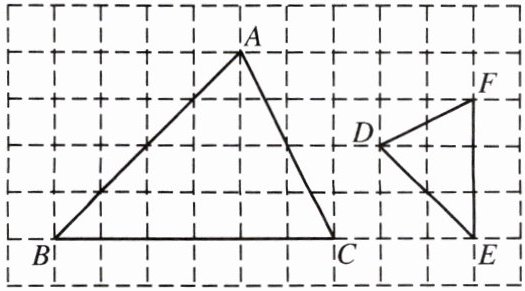
(1) 求$\frac{AB}{DE}$,$\frac{BC}{EF}$,$\frac{AC}{DF}$的值.
(2) 在 $AB$,$BC$,$AC$,$DE$,$EF$,$DF$ 这六条线段中,找出三组比例线段.

答案:
6.解:
(1)
∵$AB = 4\sqrt{2}$,$BC = 6$,$AC = 2\sqrt{5}$,$DE = 2\sqrt{2}$,
$EF = 3$,$DF = \sqrt{5}$,
∴$\frac{AB}{DE}=2$,$\frac{BC}{EF}=2$,$\frac{AC}{DF}=2$.
(2)$\frac{AB}{DE}=\frac{BC}{EF}$,$AB$,$DE$,$BC$,$EF$是比例线段;
$\frac{AB}{DE}=\frac{AC}{DF}$,$AB$,$DE$,$AC$,$DF$是比例线段;
$\frac{BC}{EF}=\frac{AC}{DF}$,$BC$,$EF$,$AC$,$DF$是比例线段.
(1)
∵$AB = 4\sqrt{2}$,$BC = 6$,$AC = 2\sqrt{5}$,$DE = 2\sqrt{2}$,
$EF = 3$,$DF = \sqrt{5}$,
∴$\frac{AB}{DE}=2$,$\frac{BC}{EF}=2$,$\frac{AC}{DF}=2$.
(2)$\frac{AB}{DE}=\frac{BC}{EF}$,$AB$,$DE$,$BC$,$EF$是比例线段;
$\frac{AB}{DE}=\frac{AC}{DF}$,$AB$,$DE$,$AC$,$DF$是比例线段;
$\frac{BC}{EF}=\frac{AC}{DF}$,$BC$,$EF$,$AC$,$DF$是比例线段.
查看更多完整答案,请扫码查看


