《2025年名师面对面学科素养评价九年级数学全一册浙教版》

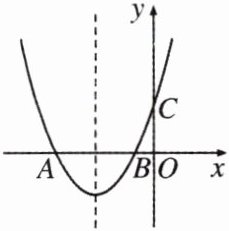
7. 如图，二次函数$y = ax^{2} + bx + c(a ＞ 0)$的图象与$x$轴交于$A$，$B$两点，与$y$轴正半轴交于点$C$，它的对称轴为直线$x = -1$.则下列选项正确的是(D)

A.$abc ＜ 0$
B.$4ac - b^{2} ＞ 0$
C.$c - a ＞ 0$
D.当$x = -n^{2} - 2$($n$为实数)时，$y \geq c$
]

答案： 7.D 【解析】A 错误;B 错误;
∵-$\frac{b}{2a}$=-1,
∴b=2a,
∵当 x=-1 时,y=a-b+c＜0,
∴a-2a+c＜0,
∴c-a＜0,C 错误;当 x=-n² - 2(n 为实数)时,y=ax² + bx + c=a(-n² - 2)² + b(-n² - 2)+c=an²(n² + 2)+c,
∵a＞0,n²≥0,n² + 2＞0,
∴y=an²(n² + 2)+c≥c,D 正确.

8. 已知关于$x$的一元二次方程$mx^{2} + (1 - 5m)x - 5 = 0(m \neq 0)$.
(1) 求证：无论$m$为何非零实数，此方程总有两个实数根.
(2) 若抛物线$y = mx^{2} + (1 - 5m)x - 5$与$x$轴交于$A(x_{1},0)$，$B(x_{2},0)$两点，且$|x_{1} - x_{2}| = 6$，求$m$的值.

答案： 8.
(1)证明：由题意可得：Δ=(1 - 5m)² - 4m×(-5)=1 + 25m² - 10m + 20m=25m² + 10m + 1=(5m + 1)²≥0,
∴无论 m 为任何非零实数，此方程总有两个实数根.
(2)解：mx² + (1 - 5m)x - 5 = 0,解得$x_1 = -\frac{1}{m}$,$x_2 = 5$,由 |x₁ - x₂| = 6,得|$-\frac{1}{m} - 5| = 6$,解得 m=1 或 m=-$\frac{1}{11}$.

9. 小聪设计奖杯，从抛物线形状上获得灵感，在平面直角坐标系中画出截面示意图，如图1，杯体$ACB$是抛物线的一部分，抛物线的顶点$C$在$y$轴上，杯口直径$AB = 4$，且点$A$，$B$关于$y$轴对称，杯脚高$CO = 4$，杯高$DO = 8$，杯底$MN$在$x$轴上.
(1) 求杯体$ACB$所在抛物线的函数表达式（不必写出$x$的取值范围）.
(2) 为使奖杯更加美观，小敏提出了改进方案.如图2，杯体$A'CB'$所在抛物线形状不变，杯口直径$A'B' // AB$，杯脚高$CO$不变，杯深$CD'$与杯高$OD'$之比为$0.6$.求$A'B'$的长.
]

答案： 9.解：
(1)设抛物线的函数表达式为 y=ax² + 4,
由题意，得 A(-2,8),B(2,8),将 B(2,8)代入 y=ax² + 4,
得 8=a×2² + 4,解得 a=1,
∴该抛物线的函数表达式为 y=x² + 4.
(2)由题意，得$\frac{CD'}{OD'}$=0.6,CO=4,
∴$\frac{CD'}{4 + CD'}$=0.6,
∴CD'=6,
∴OD'=OC + CD'=10,又
∵杯体 A'CB'所在抛物线形状不变,杯口直径 A'B'//AB,
∴设 B'(x₁,10),A'(x₂,10),
∴当 y=10 时,10=x² + 4,解得$x_1 = \sqrt{6}$,$x_2 = -\sqrt{6}$,
∴杯口直径 A'B'的长为$2\sqrt{6}$.