1. 抛物线$y = -\frac{1}{2}x^{2} + x + 1$经平移后,不可能得到的抛物线是(
A.$y = -\frac{1}{2}x^{2} + x$
B.$y = -\frac{1}{2}x^{2} - 4$
C.$y = -\frac{1}{2}x^{2} + 2021x - 2022$
D.$y = -x^{2} + x + 1$
D
)A.$y = -\frac{1}{2}x^{2} + x$
B.$y = -\frac{1}{2}x^{2} - 4$
C.$y = -\frac{1}{2}x^{2} + 2021x - 2022$
D.$y = -x^{2} + x + 1$
答案:
1.D
2. 二次函数$y = (x + 1)^{2} - 2$的图象大致是(
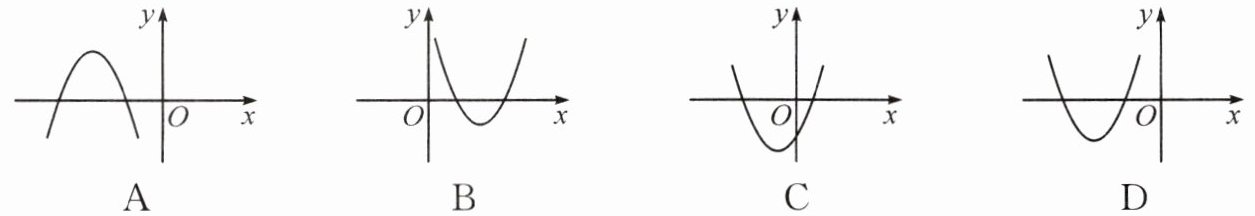
]
C
)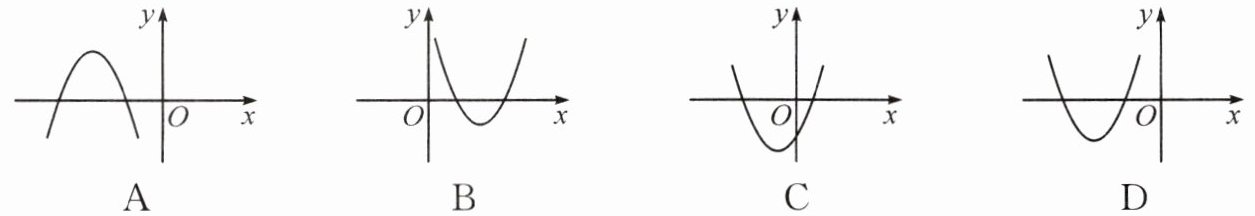
]
答案:
2.C
3. 在平面直角坐标系中,将二次函数$y = (x - 1)^{2} + 1$的图象向左平移$1$个单位长度,再向下平移$2$个单位长度,所得函数的表达式为(
A.$y = (x - 2)^{2} - 1$
B.$y = (x - 2)^{2} + 3$
C.$y = x^{2} + 1$
D.$y = x^{2} - 1$
D
)A.$y = (x - 2)^{2} - 1$
B.$y = (x - 2)^{2} + 3$
C.$y = x^{2} + 1$
D.$y = x^{2} - 1$
答案:
3.D
4. 抛物线$y = 2(x + 9)^{2} - 3$的顶点坐标是
(-9,-3)
。
答案:
4.(-9,-3)
5. 已知一个二次函数的图象开口向上,顶点坐标为$(0, -1)$,那么这个二次函数的表达式可以是
$y = 2x^{2}-1$(答案不唯一)
。
答案:
5.$y = 2x^{2}-1$(答案不唯一)
6. 在平面直角坐标系中,抛物线的函数表达式为$y = ax^{2} + 2bx + 2b - a(a \neq 0)$。
(1) 当$x = -1$时,求$y$的值。
(2) 将抛物线向左平移$2$个单位长度后,恰经过点$(-1, 0)$,求$b$的值。
(1) 当$x = -1$时,求$y$的值。
(2) 将抛物线向左平移$2$个单位长度后,恰经过点$(-1, 0)$,求$b$的值。
答案:
6.解:
(1)当$x = -1$时,$y = a - 2b + 2b - a = 0$.
(2)
∵将抛物线向左平移2个单位后,恰经过点$(-1,0)$,
∴原抛物线经过$(1,0)$,把$(1,0)$代入解析式,得$0 = a + 2b + 2b - a$,
∴$b = 0$.
(1)当$x = -1$时,$y = a - 2b + 2b - a = 0$.
(2)
∵将抛物线向左平移2个单位后,恰经过点$(-1,0)$,
∴原抛物线经过$(1,0)$,把$(1,0)$代入解析式,得$0 = a + 2b + 2b - a$,
∴$b = 0$.
查看更多完整答案,请扫码查看


