《2025年名师面对面学科素养评价九年级数学全一册浙教版》

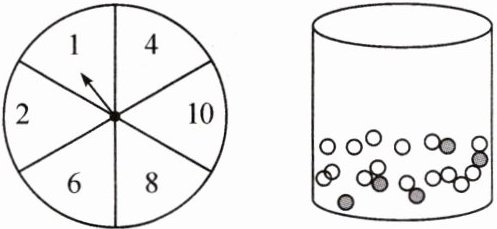
7. 春天园游会有一个摊位的游戏是先旋转一个转盘的指针,如果指针箭头停在奇数的位置,玩的人就可以从袋子中抽出一个弹珠.转盘和袋子里的弹珠如下图所示,抽到黑色的弹珠就能得到奖品.小刚玩了这个游戏,则小刚得到奖品的可能性为 (C)


A.不可能
B.非常有可能
C.不太可能
D.大约 $50\%$ 的可能

答案： 7.C

8. 在九年级一班举行的元旦联欢晚会上,同学们通过抽签决定即兴表演节目的形式,一共做了 20 张表演唱歌的签、12 张表演朗诵的签、8 张表演舞蹈的签.
(1) 第一次抽签,抽到表演唱歌和表演朗诵的可能性相同吗?
(2) 晚会进行到一半时,已经有 9 人表演唱歌、6 人表演朗诵、5 人表演舞蹈.这时轮到你去抽签,你抽到表演哪种节目的可能性最小? 为什么?

答案： 8.解：
(1)抽到表演唱歌和表演朗诵的可能性不相同．
(2)因为剩下的表演唱歌的签有$11$张，表演朗诵的签有$6$张，表演舞蹈的签有$3$张，所以抽到表演舞蹈节目的可能性最小．

9. 在四个完全相同的小球上分别写上 1,2,3,4 四个数字,然后将小球装入一个不透明的口袋内搅匀.从口袋内取出一个小球记下数字,作为点 P 的横坐标 x,放回袋中搅匀,然后再从袋中取出一个小球记下数字,作为点 P 的纵坐标 y.
(1) 点 P 的坐标有多少种可能的结果?
(2) 点 $P(x,y)$ 落在直线 $y = -x + 5$ 上的可能性有多大?

答案： 9.解：
(1)点$P$的坐标共有$16$种等可能的结果．
(2)
∵共有$16$种等可能的结果，数字$x,y$满足$y = -x + 5$的有$(1,4)$，$(2,3)$，$(3,2)$，$(4,1)$四种，所以可能性为$\frac{4}{16} = \frac{1}{4}$．