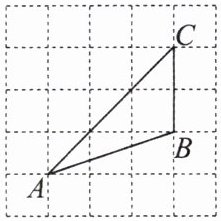
7. 如图,将 $ \triangle ABC $ 放在每个小正方形的边长为 $ 1 $ 的网格中,点 $ A $,$ B $,$ C $ 在格点上,则 $ \angle A $ 的正切值是(
A.$ \frac{\sqrt{5}}{5} $
B.$ \frac{\sqrt{10}}{5} $
C.$ 2 $
D.$ \frac{1}{2} $
]
D
)
A.$ \frac{\sqrt{5}}{5} $
B.$ \frac{\sqrt{10}}{5} $
C.$ 2 $
D.$ \frac{1}{2} $
]
答案:
7.D
8. 如图,在 $ \triangle ABC $ 中,$ \angle A $ 为钝角,$ AB = 25 $,$ AC = 39 $,$ \sin B = \frac{3}{5} $,求 $ \tan C $ 和 $ BC $ 的长。
 ]
]
 ]
]
答案:
8.解:过点A作AD⊥BC于D,如图所示.

在Rt△ABD中,AB=25,sinB=$\frac{AD}{AB}$=$\frac{3}{5}$,
∴$\frac{AD}{25}$=$\frac{3}{5}$,
∴AD=15,
在Rt△ACD中,CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{39^{2}-15^{2}} = 36$,
∴tanC=$\frac{AD}{CD}$=$\frac{15}{36}$=$\frac{5}{12}$;
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{25^{2}-15^{2}} = 20$,
∴BC=BD+CD=20+36=56.
8.解:过点A作AD⊥BC于D,如图所示.

在Rt△ABD中,AB=25,sinB=$\frac{AD}{AB}$=$\frac{3}{5}$,
∴$\frac{AD}{25}$=$\frac{3}{5}$,
∴AD=15,
在Rt△ACD中,CD=$\sqrt{AC^{2}-AD^{2}}=\sqrt{39^{2}-15^{2}} = 36$,
∴tanC=$\frac{AD}{CD}$=$\frac{15}{36}$=$\frac{5}{12}$;
在Rt△ABD中,BD=$\sqrt{AB^{2}-AD^{2}}=\sqrt{25^{2}-15^{2}} = 20$,
∴BC=BD+CD=20+36=56.
9. 阅读下列材料:
在 $ \triangle ABC $ 中,$ \angle A $,$ \angle B $,$ \angle C $ 所对的边分别为 $ a $,$ b $,$ c $。求证:$ \frac{a}{\sin A} = \frac{b}{\sin B} $。
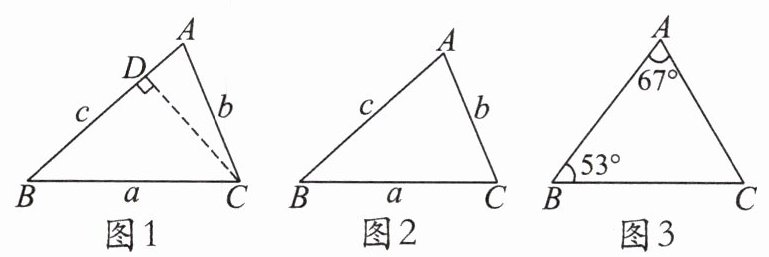
证明:如图 $ 1 $,过点 $ C $ 作 $ CD \perp AB $ 于点 $ D $,
在 $ Rt\triangle BCD $ 中,$ CD = a\sin B $,
在 $ Rt\triangle ACD $ 中,$ CD = b\sin A $,
$ \therefore a\sin B = b\sin A $。
$ \therefore \frac{a}{\sin A} = \frac{b}{\sin B} $。
根据上面的材料解决下列问题:
(1)如图 $ 2 $,在 $ \triangle ABC $ 中,$ \angle A $,$ \angle B $,$ \angle C $ 所对的边分别为 $ a $,$ b $,$ c $。求证:$ \frac{b}{\sin B} = \frac{c}{\sin C} $。
(2)如图 $ 3 $,规划中的一片三角形区域需美化。已知 $ \angle A = 67^{\circ} $,$ \angle B = 53^{\circ} $,$ AC = 80 $ 米,求这片区域的面积。(结果保留根号,参考数据:$ \sin 53^{\circ} \approx 0.8 $,$ \sin 67^{\circ} \approx 0.9 $)
]
在 $ \triangle ABC $ 中,$ \angle A $,$ \angle B $,$ \angle C $ 所对的边分别为 $ a $,$ b $,$ c $。求证:$ \frac{a}{\sin A} = \frac{b}{\sin B} $。
证明:如图 $ 1 $,过点 $ C $ 作 $ CD \perp AB $ 于点 $ D $,
在 $ Rt\triangle BCD $ 中,$ CD = a\sin B $,
在 $ Rt\triangle ACD $ 中,$ CD = b\sin A $,
$ \therefore a\sin B = b\sin A $。
$ \therefore \frac{a}{\sin A} = \frac{b}{\sin B} $。
根据上面的材料解决下列问题:
(1)如图 $ 2 $,在 $ \triangle ABC $ 中,$ \angle A $,$ \angle B $,$ \angle C $ 所对的边分别为 $ a $,$ b $,$ c $。求证:$ \frac{b}{\sin B} = \frac{c}{\sin C} $。
(2)如图 $ 3 $,规划中的一片三角形区域需美化。已知 $ \angle A = 67^{\circ} $,$ \angle B = 53^{\circ} $,$ AC = 80 $ 米,求这片区域的面积。(结果保留根号,参考数据:$ \sin 53^{\circ} \approx 0.8 $,$ \sin 67^{\circ} \approx 0.9 $)
]

答案:
9.
(1)证明:如图2,过点A作AD⊥BC于点D,
在Rt△ABD中,AD=csinB,在Rt△ACD中,
AD=bsinC,
∴csinB=bsinC,
∴$\frac{b}{sinB}$=$\frac{c}{sinC}$.



(2)解:如图3,过点A作AE⊥BC于点E,
∵∠BAC=67°,∠B=53°,
∴∠C=60°,
在Rt△ACE中,AE=AC·sin60°=80×$\frac{\sqrt{3}}{2}$=40$\sqrt{3}$(m),又
∵$\frac{AC}{sinB}$=$\frac{BC}{sin\angle BAC}$,即$\frac{80}{0.8}$=$\frac{BC}{0.9}$,
∴BC=90(m),
∴S△ABC=$\frac{1}{2}$×90×40$\sqrt{3}$=1800$\sqrt{3}$(m²).
9.
(1)证明:如图2,过点A作AD⊥BC于点D,
在Rt△ABD中,AD=csinB,在Rt△ACD中,
AD=bsinC,
∴csinB=bsinC,
∴$\frac{b}{sinB}$=$\frac{c}{sinC}$.



(2)解:如图3,过点A作AE⊥BC于点E,
∵∠BAC=67°,∠B=53°,
∴∠C=60°,
在Rt△ACE中,AE=AC·sin60°=80×$\frac{\sqrt{3}}{2}$=40$\sqrt{3}$(m),又
∵$\frac{AC}{sinB}$=$\frac{BC}{sin\angle BAC}$,即$\frac{80}{0.8}$=$\frac{BC}{0.9}$,
∴BC=90(m),
∴S△ABC=$\frac{1}{2}$×90×40$\sqrt{3}$=1800$\sqrt{3}$(m²).
查看更多完整答案,请扫码查看


