1. 利用计算器求 $ \sin 30^{\circ} $ 时,依次按键 ,则计算器上显示的结果是 (
A.$ 0.5 $
B.$ 0.707 $
C.$ 0.866 $
D.$ 1 $
A
)A.$ 0.5 $
B.$ 0.707 $
C.$ 0.866 $
D.$ 1 $
答案:
1.A
2. 我们数学课本上采用的科学计算器面板如图所示,利用该型号计算器计算 $ \sqrt{2} \cos 55^{\circ} $,按键顺序正确的是 (

A.
B.
C.
D.
C
)
A.
B.
C.
D.
答案:
2.C
3. 如图,已知 $ AB $ 是 $ \odot O $ 的直径,$ CD $ 是 $ \odot O $ 的弦,$ AB \perp CD $,垂足为 $ E $。若 $ AB = 26 $,$ CD = 24 $,则 $ \angle OCE $ 的余弦值为 (

A.$ \dfrac{7}{13} $
B.$ \dfrac{12}{13} $
C.$ \dfrac{7}{12} $
D.$ \dfrac{13}{12} $
B
)
A.$ \dfrac{7}{13} $
B.$ \dfrac{12}{13} $
C.$ \dfrac{7}{12} $
D.$ \dfrac{13}{12} $
答案:
3.B
4. 某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆 $ AB $ 的长为 (
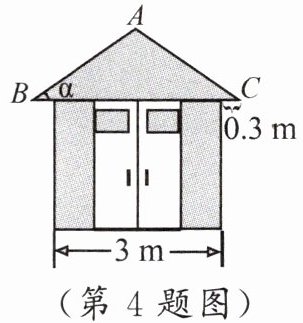
A.$ \dfrac{9}{5 \sin \alpha} m $
B.$ \dfrac{9}{5 \cos \alpha} m $
C.$ \dfrac{5}{9 \sin \alpha} m $
D.$ \dfrac{5}{9 \cos \alpha} m $
B
)
A.$ \dfrac{9}{5 \sin \alpha} m $
B.$ \dfrac{9}{5 \cos \alpha} m $
C.$ \dfrac{5}{9 \sin \alpha} m $
D.$ \dfrac{5}{9 \cos \alpha} m $
答案:
4.B
5. 计算:
(1) $ \sin 60^{\circ} \cdot \cos 30^{\circ} - \dfrac{1}{2} $。
(2) $ 2 \cos ^{2} 30^{\circ} - 2 \sin 60^{\circ} \cdot \cos 45^{\circ} $。
(3) $ 2 \sin 30^{\circ} - 3 \tan 45^{\circ} + 4 \cos 60^{\circ} $。
(1) $ \sin 60^{\circ} \cdot \cos 30^{\circ} - \dfrac{1}{2} $。
(2) $ 2 \cos ^{2} 30^{\circ} - 2 \sin 60^{\circ} \cdot \cos 45^{\circ} $。
(3) $ 2 \sin 30^{\circ} - 3 \tan 45^{\circ} + 4 \cos 60^{\circ} $。
答案:
5.解:
(1)原式$=\frac{\sqrt{3}}{2} × \frac{\sqrt{3}}{2} - \frac{1}{2} = \frac{1}{4}。$
(2)原式$=2 × (\frac{\sqrt{3}}{2})^{2} - 2 × \frac{\sqrt{3}}{2} × \frac{\sqrt{2}}{2} = \frac{3 - \sqrt{6}}{2}。$
(3)原式$=2 × \frac{1}{2} - 3 × 1 + 4 × \frac{1}{2} = 0。$
(1)原式$=\frac{\sqrt{3}}{2} × \frac{\sqrt{3}}{2} - \frac{1}{2} = \frac{1}{4}。$
(2)原式$=2 × (\frac{\sqrt{3}}{2})^{2} - 2 × \frac{\sqrt{3}}{2} × \frac{\sqrt{2}}{2} = \frac{3 - \sqrt{6}}{2}。$
(3)原式$=2 × \frac{1}{2} - 3 × 1 + 4 × \frac{1}{2} = 0。$
6. 如图,将 $ 45^{\circ} $ 的 $ \angle AOB $ 按图中的方式放置在一把刻度尺上,定点 $ O $ 与尺下沿的端点重合,$ OA $ 与尺下沿重合,$ OB $ 与尺上沿的交点 $ B $ 在刻度尺上的读数恰为 $ 2 cm $。若按相同的方式将 $ 37^{\circ} $ 的 $ \angle AOC $ 放置在该刻度尺上,则 $ OC $ 与尺上沿的交点 $ C $ 在尺上的读数为
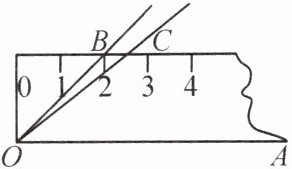
2.7
$ cm $。(结果精确到 $ 0.1 cm $,参考数据:$ \sin 37^{\circ} \approx 0.60 $,$ \cos 37^{\circ} \approx 0.80 $,$ \tan 37^{\circ} \approx 0.75 $)
答案:
6.2.7
查看更多完整答案,请扫码查看


