《2025年名师面对面学科素养评价九年级数学全一册浙教版》

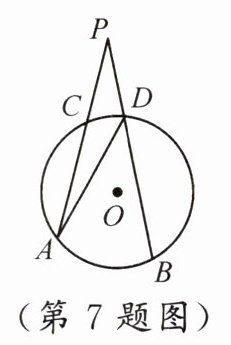
7. 如图，$P$是$\odot O$外一点，$PA$，$PB$分别交$\odot O$于$C$，$D$两点，已知$\overgroup{AB}$和$\overgroup{CD}$所对的圆心角分别为$90^{\circ}$和$50^{\circ}$，则$\angle P =$(D)

A.$45^{\circ}$
B.$40^{\circ}$
C.$25^{\circ}$
D.$20^{\circ}$

答案： 7.D

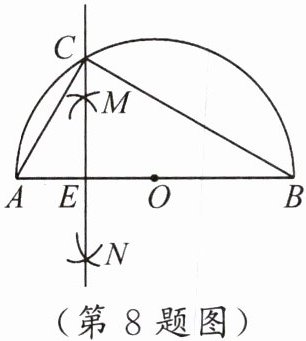
8. 如图，线段$AB$是半圆$O$的直径，分别以点$A$和点$O$为圆心、大于$\frac{1}{2}AO$的长为半径作弧，两弧交于$M$，$N$两点，作直线$MN$，交半圆$O$于点$C$，交$AB$于点$E$，连结$AC$，$BC$.若$AE = 1$，则$BC$的长是2√3.

答案： 8.$2\sqrt{3}$

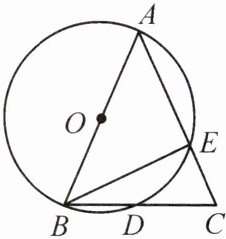
9. 如图，在$\triangle ABC$中，$AB = AC$，$\angle BAC = 45^{\circ}$，以$AB$为直径的$\odot O$交$BC$于点$D$，交$AC$于点$E$.
（1）求$\angle EBC$的度数.
（2）求证：$BD = CD$.

答案：
9.解：
(1)
∵AB = AC，
∴∠ABC = ∠C，
∴∠C = $\frac{1}{2}(180^{\circ} - ∠BAC) = 67.5^{\circ}$，
∵AB 为直径，
∴∠AEB = $90^{\circ}$，
∵∠AEB = ∠EBC + ∠C，
∴∠EBC = $90^{\circ} - 67.5^{\circ} = 22.5^{\circ}$.
(2)证明：连结 AD，如图，
∵AB 为直径，

∴∠ADB = $90^{\circ}$，即 AD ⊥ BC，
∵AB = AC，
∴BD = CD.

10. 如图，$\triangle ABC$是$\odot O$的内接三角形，点$C$是优弧$AB$上一点，设$\angle OAB = \alpha$，$\angle C = \beta$.
（1）猜想$\beta$关于$\alpha$的函数表达式，并给出证明.
（2）若$\alpha = 30^{\circ}$，$AB = 6$，$S_{\triangle ABC} = 6\sqrt{3}$，求$AC$的长.

答案：
10.解：
(1)如图 1，结论：$\beta = 90^{\circ} - \alpha$.
理由：连结 OB.
∵OA = OB，
∴∠OAB = ∠OBA = $\alpha$，
∴∠AOB = $180^{\circ} - 2\alpha$，
∴∠C = $\frac{1}{2}$∠AOB = $90^{\circ} - \alpha$，即$\beta = 90^{\circ} - \alpha$.

(2)如图 2，延长 AO 交⊙O 于 E，连结 EB，作 EF // AB 交⊙O 于 F，连结 AF.
∵AE 是直径，
∴∠ABE = $90^{\circ}$，
∵∠EAB = $30^{\circ}$，AB = 6，
∴BE = $2\sqrt{3}$，
∴$S_{\triangle EAB} = \frac{1}{2} \cdot AB \cdot EB = 6\sqrt{3}$，
∵$S_{\triangle ABC} = 6\sqrt{3}$，
∴点 C 与 E 重合或与 F 重合，
∴AC = 2BE = $4\sqrt{3}$或$AC' = AF = BE = 2\sqrt{3}$.
综上所述，AC 的长度为$4\sqrt{3}$或$2\sqrt{3}$.