《2025年名师面对面学科素养评价九年级数学全一册浙教版》

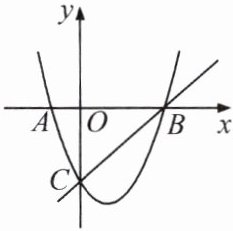
1. 如图，已知抛物线 $ y = ax^{2} - x + c $ 与 $ x $ 轴相交于 $ A $，$ B $ 两点，并与直线 $ y = x - 2 $ 交于 $ B $，$ C $ 两点，其中点 $ C $ 是直线 $ y = x - 2 $ 与 $ y $ 轴的交点.
(1) 求点 $ B $，点 $ C $ 的坐标.
(2) 求抛物线的函数表达式.

答案： 1.解：
(1)
∵直线 y=x-2 交 x 轴、y 轴于 B,C 两点，
∴B(2,0),C(0,-2).
(2)
∵$y=ax^{2}-x+c $过 B,C 两点，
将 B,C 坐标代入抛物线的解析式，
可求得 a=1,c=-2.
∴抛物线的解析式为$ y=x^{2}-x-2.$

2. 二次函数 $ y = ax^{2} + bx + c $ 的对称轴为直线 $ x = 3 $，最小值为 $ - 2 $，且过 $ (0,1) $，求此二次函数的表达式.

答案： 2.解：
∵二次函数$ y=ax^{2}+bx+c $的对称轴为 x=3，最小值为 -2，
∴二次函数的顶点坐标为(3,-2).
设二次函数为$ y=a(x-3)^{2}-2，$
∵抛物线经过(0,1)，
∴9a-2=1，解得$ a=\frac{1}{3}. $
∴此二次函数的表达式为$ y=\frac{1}{3}(x-3)^{2}-2.$