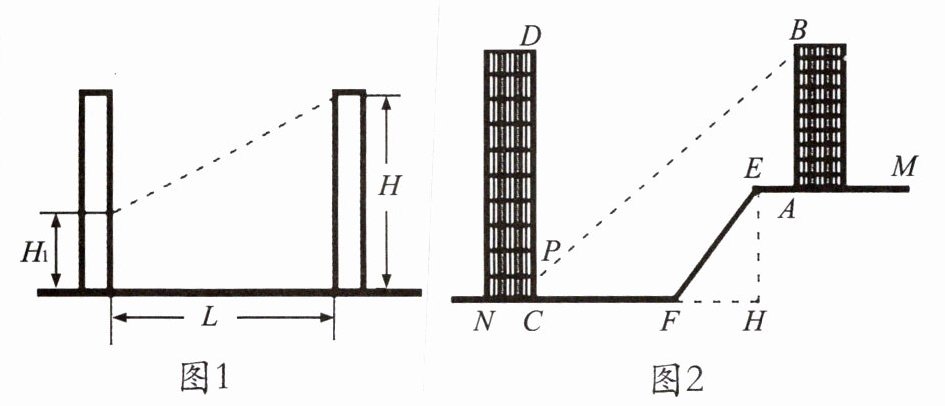
7. 日照间距系数反映了房屋日照情况。如图 1,当前后房屋都朝向正南时,日照间距系数 $= L:(H - H_1)$,其中 $L$ 为楼间水平距离,$H$ 为南侧楼房高度,$H_1$ 为北侧楼房底层窗台至地面高度。如图 2,山坡 $EF$ 朝北,$EF$ 长为 $15m$,坡度为 $i = 1:0.75$,山坡顶部平地 $EM$ 上有一高为 $22.5m$ 的楼房 $AB$,底部 $A$ 到 $E$ 点的距离为 $4m$。
(1) 求山坡 $EF$ 的水平宽度 $FH$。
(2) 欲在楼房 $AB$ 正北侧山脚的平地 $FN$ 上建一楼房 $CD$,已知该楼底层窗台 $P$ 处至地面 $C$ 处的高度为 $0.9m$,要使该楼的日照间距系数不低于 $1.25$,底部 $C$ 距 $F$ 处至少多远?
(1) 求山坡 $EF$ 的水平宽度 $FH$。
(2) 欲在楼房 $AB$ 正北侧山脚的平地 $FN$ 上建一楼房 $CD$,已知该楼底层窗台 $P$ 处至地面 $C$ 处的高度为 $0.9m$,要使该楼的日照间距系数不低于 $1.25$,底部 $C$ 距 $F$ 处至少多远?

答案:
7.解:
(1)在 Rt△EFH 中,
∵∠H=90°,
∴tan∠EFH=i=1:0.75= $\frac{4}{3}=\frac{EH}{FH}$,
设 EH=4x,则 FH=3x,
∴EF= $\sqrt{EH^{2}+FH^{2}}=5x$,
∵EF=15,
∴5x=15,x=3,
∴FH=3x=9.
即山坡 EF 的水平宽度 FH 为 9 m.


(2)
∵L=CF+FH+EA=CF+9+4=CF+13,
H=AB+EH=22.5+12=34.5,H₁=0.9,
∴日照间距系数=L:(H - H₁)=$\frac{CF+13}{34.5 - 0.9}=\frac{CF+13}{33.6}$,
∵该楼的日照间距系数不低于 1.25,
∴$\frac{CF+13}{33.6}≥1.25$,
∴CF≥29.
答:要使该楼的日照间距系数不低于 1.25,底部 C 至少距 F 处 29 m 远.
7.解:
(1)在 Rt△EFH 中,
∵∠H=90°,
∴tan∠EFH=i=1:0.75= $\frac{4}{3}=\frac{EH}{FH}$,
设 EH=4x,则 FH=3x,
∴EF= $\sqrt{EH^{2}+FH^{2}}=5x$,
∵EF=15,
∴5x=15,x=3,
∴FH=3x=9.
即山坡 EF 的水平宽度 FH 为 9 m.


(2)
∵L=CF+FH+EA=CF+9+4=CF+13,
H=AB+EH=22.5+12=34.5,H₁=0.9,
∴日照间距系数=L:(H - H₁)=$\frac{CF+13}{34.5 - 0.9}=\frac{CF+13}{33.6}$,
∵该楼的日照间距系数不低于 1.25,
∴$\frac{CF+13}{33.6}≥1.25$,
∴CF≥29.
答:要使该楼的日照间距系数不低于 1.25,底部 C 至少距 F 处 29 m 远.
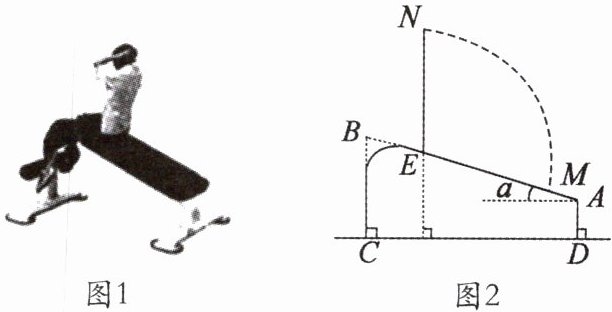
8. 图 1 是小明在健身器材上进行仰卧起坐锻炼时情景,图 2 是小明锻炼时上半身由 $EM$ 位置运动到与地面垂直的 $EN$ 位置时的示意图,已知:$BC \perp CD$,$AD \perp CD$,$BC = 0.64m$,$AD = 0.24m$,$AB = 1.29m$。
(1) 求 $AB$ 的倾斜角 $\alpha$ 的度数。(结果精确到 $1^{\circ}$,参考数据:$\sin 17^{\circ} \approx 0.2924$,$\sin 18^{\circ} \approx 0.3090$,$\sin 19^{\circ} \approx 0.3256$)
(2) 若测得 $EN = 0.88m$,试计算小明头顶由 $M$ 点运动到 $N$ 点的路径弧 $MN$ 的长度。(结果精确到 $0.01m$)
(1) 求 $AB$ 的倾斜角 $\alpha$ 的度数。(结果精确到 $1^{\circ}$,参考数据:$\sin 17^{\circ} \approx 0.2924$,$\sin 18^{\circ} \approx 0.3090$,$\sin 19^{\circ} \approx 0.3256$)
(2) 若测得 $EN = 0.88m$,试计算小明头顶由 $M$ 点运动到 $N$ 点的路径弧 $MN$ 的长度。(结果精确到 $0.01m$)

答案:
8.解:
(1)过 A 作 AF//DC,分别交 BC,NE 的延长线于 F,H,
∵AD⊥CD,BC⊥CD,
∴AD//BC,
∴四边形 AFCD 为矩形,
∴BF=BC - AD=0.4.
在 Rt△ABF 中,
∵sinα=$\frac{BF}{AB}=\frac{0.4}{1.29}≈0.310$,
∴α≈18°.即 AB 的倾斜角度数约为 18°.
(2)
∵NE⊥AF,
∴∠AEH=90° - 18°=72°.
∴∠MEN=180° - ∠AEH=108°.
∴弧 MN 的长=$\frac{108π×0.88}{180}≈1.66$(米).
答:小明头顶运动的路径 $\overset{\frown}{MN}$ 的长约为 1.66 米.
(1)过 A 作 AF//DC,分别交 BC,NE 的延长线于 F,H,
∵AD⊥CD,BC⊥CD,
∴AD//BC,
∴四边形 AFCD 为矩形,
∴BF=BC - AD=0.4.
在 Rt△ABF 中,
∵sinα=$\frac{BF}{AB}=\frac{0.4}{1.29}≈0.310$,
∴α≈18°.即 AB 的倾斜角度数约为 18°.
(2)
∵NE⊥AF,
∴∠AEH=90° - 18°=72°.
∴∠MEN=180° - ∠AEH=108°.
∴弧 MN 的长=$\frac{108π×0.88}{180}≈1.66$(米).
答:小明头顶运动的路径 $\overset{\frown}{MN}$ 的长约为 1.66 米.
查看更多完整答案,请扫码查看


