7. 如图,点 $O$ 为线段 $BC$ 的中点,点 $A$,$C$,$D$ 到点 $O$ 的距离相等. 若 $\angle ABC = 40^{\circ}$,则 $\angle ADC$ 的度数是(
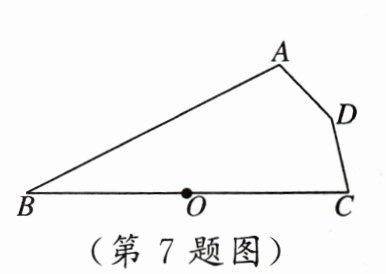
A.$130^{\circ}$
B.$140^{\circ}$
C.$150^{\circ}$
D.$160^{\circ}$
B
)
A.$130^{\circ}$
B.$140^{\circ}$
C.$150^{\circ}$
D.$160^{\circ}$
答案:
7.B
8. 如图,四边形 $ABCD$ 是菱形,$\odot O$ 经过点 $A$,$C$,$D$,与 $BC$ 相交于点 $E$,连结 $AC$,$AE$. 若 $\angle D = 70^{\circ}$,则 $\angle EAC$ 的度数为
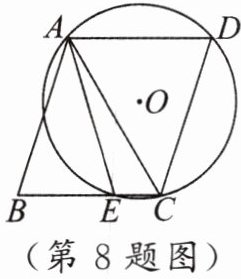
15°
.
答案:
8.15°
9. 如图,四边形 $ABCD$ 内接于 $\odot O$,$E$ 为 $BC$ 延长线上一点,连结 $AC$,$BD$. 若 $DA = DB$,求证:$CD$ 平分 $\angle ACE$.


答案:
9.证明:
∵四边形ABCD内接于⊙O,易证∠DAB=∠DCE.
∵DA=DB,
∴∠DAB=∠DBA,
∴∠DBA=∠DCE.
∵∠DBA与∠DCA是同弧所对的圆周角,
∴∠DBA=∠DCA,
∴∠DCA=∠DCE,即CD平分∠ACE.
∵四边形ABCD内接于⊙O,易证∠DAB=∠DCE.
∵DA=DB,
∴∠DAB=∠DBA,
∴∠DBA=∠DCE.
∵∠DBA与∠DCA是同弧所对的圆周角,
∴∠DBA=∠DCA,
∴∠DCA=∠DCE,即CD平分∠ACE.
10. 如图,在 $\odot O$ 中,$B$ 是 $\odot O$ 上的一点,$\angle ABC = 120^{\circ}$,弦 $AC = 2\sqrt{3}$,弦 $BM$ 平分 $\angle ABC$ 交 $AC$ 于点 $D$,连结 $MA$,$MC$.
(1)求 $\odot O$ 半径的长.
(2)求证:$AB + BC = BM$.

(1)求 $\odot O$ 半径的长.
(2)求证:$AB + BC = BM$.

答案:
10.
(1)解:
∵∠ABC=120°,BM平分∠ABC,
∴∠MBA=∠MBC=$\frac{1}{2}$∠ABC=60°.
∴∠ACM=∠ABM=60°.∠MAC=∠MBC=60°.
∴在△AMC中,∠AMC=60°.
∴△AMC是等边三角形.
如图,连结OA,OC,过点O作OH⊥AC于点H.
∴AO=CO,∠AOC=2∠AMC=120°.
∴∠OAC=∠OCA=30°,
∴AH=CH=$\frac{1}{2}$AC=$\sqrt{3}$
∴在Rt△AOH中,AO=2,
∴⊙O的半径为2.
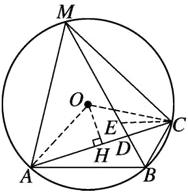
(2)证明:如图,在BM上截取BE=BC,连结CE,
∵∠MBC=60°,BE=BC,
∴△EBC为等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠ACM=60°,
∴∠ECM+∠DCE=60°.
∴∠ECM=∠BCD.又
∵AC=MC,
∴△ACB≌△MCE(SAS).
∴AB=ME.
∵ME+EB=BM,
∴AB+BC=BM.
10.
(1)解:
∵∠ABC=120°,BM平分∠ABC,
∴∠MBA=∠MBC=$\frac{1}{2}$∠ABC=60°.
∴∠ACM=∠ABM=60°.∠MAC=∠MBC=60°.
∴在△AMC中,∠AMC=60°.
∴△AMC是等边三角形.
如图,连结OA,OC,过点O作OH⊥AC于点H.
∴AO=CO,∠AOC=2∠AMC=120°.
∴∠OAC=∠OCA=30°,
∴AH=CH=$\frac{1}{2}$AC=$\sqrt{3}$
∴在Rt△AOH中,AO=2,
∴⊙O的半径为2.

(2)证明:如图,在BM上截取BE=BC,连结CE,
∵∠MBC=60°,BE=BC,
∴△EBC为等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°,
∵∠ACM=60°,
∴∠ECM+∠DCE=60°.
∴∠ECM=∠BCD.又
∵AC=MC,
∴△ACB≌△MCE(SAS).
∴AB=ME.
∵ME+EB=BM,
∴AB+BC=BM.
查看更多完整答案,请扫码查看


