8. 问题背景:
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论。如图1,已知$AD$是$\triangle ABC$的角平分线,可证$\frac{AB}{AC}=\frac{BD}{CD}$。小慧的证明思路是:如图2,过点$C$作$CE// AB$,交$AD$的延长线于点$E$,构造相似三角形来证明$\frac{AB}{AC}=\frac{BD}{CD}$。
尝试证明:
(1) 请参照小慧提供的思路,利用图2证明$\frac{AB}{AC}=\frac{BD}{CD}$。
应用拓展:
(2) 如图3,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$D$是边$BC$上一点。连结$AD$,将$\triangle ACD$沿$AD$所在直线折叠,点$C$恰好落在边$AB$上的$E$点处。若$AC = 1$,$AB = 2$,求$DE$的长。
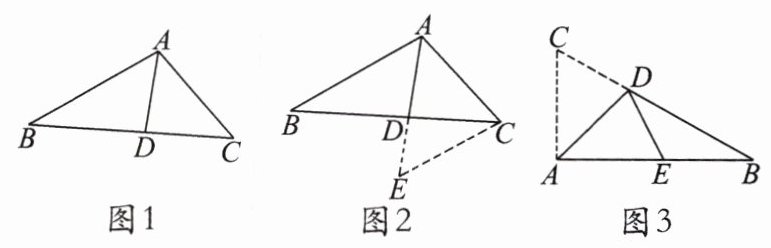
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论。如图1,已知$AD$是$\triangle ABC$的角平分线,可证$\frac{AB}{AC}=\frac{BD}{CD}$。小慧的证明思路是:如图2,过点$C$作$CE// AB$,交$AD$的延长线于点$E$,构造相似三角形来证明$\frac{AB}{AC}=\frac{BD}{CD}$。
尝试证明:
(1) 请参照小慧提供的思路,利用图2证明$\frac{AB}{AC}=\frac{BD}{CD}$。
应用拓展:
(2) 如图3,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$D$是边$BC$上一点。连结$AD$,将$\triangle ACD$沿$AD$所在直线折叠,点$C$恰好落在边$AB$上的$E$点处。若$AC = 1$,$AB = 2$,求$DE$的长。

答案:
8.
(1)证明:
∵CE//AB,
∴△CED∽△BAD,
∴$\frac{CE}{AB} = \frac{CD}{BD}$,
又
∵AD平分∠BAC,
∴∠BAD = ∠CAD,
∵CE//AB,
∴∠CED = ∠BAD,则∠CAD = ∠CED,
∴AC = CE,即$\frac{AC}{AB} = \frac{CD}{BD}$.
(2)由题意,得∠CAD = ∠BAD,CD = DE,由
(1)知,
$\frac{AC}{AB} = \frac{CD}{BD}$,即$\frac{1}{2} = \frac{CD}{BD}$,
∴BD = 2CD,又
∵∠BAC = 90°,
∴BC = $\sqrt{2^2 + 1^2} = \sqrt{5}$,即BD + CD = 3CD = $\sqrt{5}$,
∴CD = $\frac{\sqrt{5}}{3}$,即DE = $\frac{\sqrt{5}}{3}$.
(1)证明:
∵CE//AB,
∴△CED∽△BAD,
∴$\frac{CE}{AB} = \frac{CD}{BD}$,
又
∵AD平分∠BAC,
∴∠BAD = ∠CAD,
∵CE//AB,
∴∠CED = ∠BAD,则∠CAD = ∠CED,
∴AC = CE,即$\frac{AC}{AB} = \frac{CD}{BD}$.
(2)由题意,得∠CAD = ∠BAD,CD = DE,由
(1)知,
$\frac{AC}{AB} = \frac{CD}{BD}$,即$\frac{1}{2} = \frac{CD}{BD}$,
∴BD = 2CD,又
∵∠BAC = 90°,
∴BC = $\sqrt{2^2 + 1^2} = \sqrt{5}$,即BD + CD = 3CD = $\sqrt{5}$,
∴CD = $\frac{\sqrt{5}}{3}$,即DE = $\frac{\sqrt{5}}{3}$.
9. 如图,四边形$ABCD$内接于圆$O$,$AB$是直径,$C$是$\overset{\frown}{BD}$的中点,延长$AD$交$BC$的延长线于点$E$。
(1) 求证:$CE = CD$。
(2) 若$AB = 3$,$BC = \sqrt{3}$,求$AD$的长。
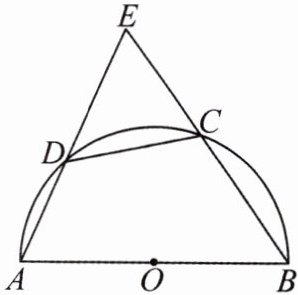
(1) 求证:$CE = CD$。
(2) 若$AB = 3$,$BC = \sqrt{3}$,求$AD$的长。

答案:
9.
(1)证明:连结AC,
∵AB为直径,
∴∠ACB = ∠ACE = 90°,又
∵点C是$\overset{\frown}{BD}$的中点,
∴∠CAE = ∠CAB,CD = CB,又
∵AC = AC,
∴△ACE≌△ACB (ASA),
∴CE = CB,
∴CE = CD.

(2)解:
∵△ACE≌△ACB,AB = 3,
∴AE = AB = 3,
又
∵四边形ABCD内接于圆O,
∴∠ADC + ∠ABC = 180°,又
∵∠ADC + ∠CDE = 180°,
∴∠CDE = ∠ABE,
又
∵∠E = ∠E,
∴△EDC∽△EBA,
∴$\frac{DE}{BE} = \frac{CD}{AB}$,
即$\frac{DE}{2\sqrt{3}} = \frac{\sqrt{3}}{3}$,解得DE = 2,
∴AD = AE−DE = 1.
9.
(1)证明:连结AC,
∵AB为直径,
∴∠ACB = ∠ACE = 90°,又
∵点C是$\overset{\frown}{BD}$的中点,
∴∠CAE = ∠CAB,CD = CB,又
∵AC = AC,
∴△ACE≌△ACB (ASA),
∴CE = CB,
∴CE = CD.

(2)解:
∵△ACE≌△ACB,AB = 3,
∴AE = AB = 3,
又
∵四边形ABCD内接于圆O,
∴∠ADC + ∠ABC = 180°,又
∵∠ADC + ∠CDE = 180°,
∴∠CDE = ∠ABE,
又
∵∠E = ∠E,
∴△EDC∽△EBA,
∴$\frac{DE}{BE} = \frac{CD}{AB}$,
即$\frac{DE}{2\sqrt{3}} = \frac{\sqrt{3}}{3}$,解得DE = 2,
∴AD = AE−DE = 1.
查看更多完整答案,请扫码查看


