7. 已知等腰$\triangle ABC$的三个顶点都在半径为$5$的$\odot O$上,如果底边$BC$的长为$8$,那么$BC$边上的高为(
A.$2$
B.$8$
C.$2$或$8$
D.$3$
C
)A.$2$
B.$8$
C.$2$或$8$
D.$3$
答案:
7.C
8. 如图,$\odot O$的半径是$4$,$\triangle ABC$是$\odot O$的内接三角形,过圆心$O$分别作$AB$,$BC$,$AC$的垂线,垂足为$E$,$F$,$G$,连结$EF$.若$OG = 1$,求线段$EF$的长.
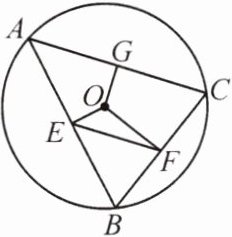

答案:
8.解:连结OC,如图,
∵OG⊥AC,
∴CG=AG,
在Rt△OCG中,CG=$\sqrt{OC² - OG²}$ = $\sqrt{15}$,
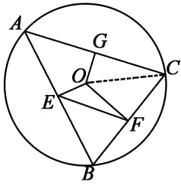
∴AC=2CG=2$\sqrt{15}$,
∵OE⊥AB,OF⊥BC,
∴AE=BE,BF=CF,
∴EF为△BAC的中位线,
∴EF=$\frac{1}{2}$AC=$\sqrt{15}$.
8.解:连结OC,如图,
∵OG⊥AC,
∴CG=AG,
在Rt△OCG中,CG=$\sqrt{OC² - OG²}$ = $\sqrt{15}$,

∴AC=2CG=2$\sqrt{15}$,
∵OE⊥AB,OF⊥BC,
∴AE=BE,BF=CF,
∴EF为△BAC的中位线,
∴EF=$\frac{1}{2}$AC=$\sqrt{15}$.
9. 如图,在半径为$5$的扇形$AOB$中,$\angle AOB = 90^{\circ}$,$C$是$\overset{\frown}{AB}$上的一个动点(不与点$A$,$B$重合),$OD\perp BC$,$OE\perp AC$,垂足分别为$D$,$E$.
(1) 若$BC = 6$,求线段$OD$的长.
(2) 在$\triangle DOE$中是否存在长度保持不变的边?度数保持不变的角?如果存在,请指出并求出其相应的长度或角度;如果不存在,请说明理由.
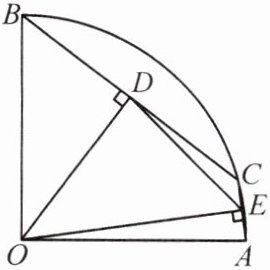
(1) 若$BC = 6$,求线段$OD$的长.
(2) 在$\triangle DOE$中是否存在长度保持不变的边?度数保持不变的角?如果存在,请指出并求出其相应的长度或角度;如果不存在,请说明理由.

答案:
9.解:
(1)
∵OD⊥BC,
∴BD=3.
∵∠BDO=90°,OB=5,BD=3,
∴OD=$\sqrt{OB²−BD²}$=4.
(2)存在,DE的长保持不变,∠DOE的度数保持不变.如图,连结AB.
∵∠AOB=90°,OA=OB=5,
∴AB=$\sqrt{OB²+OA²}$=5$\sqrt{2}$.
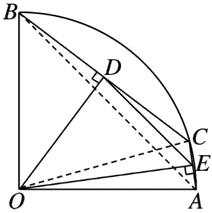
∵OD⊥BC,OE⊥AC,
∴D,E分别是线段BC,AC的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AB=$\frac{5\sqrt{2}}{2}$.连结OC.
∵OD⊥BC,OE⊥AC,OB=OC=OA,
∴∠BOD=∠COD,∠AOE=∠COE.
∵∠AOB=90°,
∴∠DOE=∠COD+∠COE=$\frac{1}{2}$∠AOB=45°.
9.解:
(1)
∵OD⊥BC,
∴BD=3.
∵∠BDO=90°,OB=5,BD=3,
∴OD=$\sqrt{OB²−BD²}$=4.
(2)存在,DE的长保持不变,∠DOE的度数保持不变.如图,连结AB.
∵∠AOB=90°,OA=OB=5,
∴AB=$\sqrt{OB²+OA²}$=5$\sqrt{2}$.

∵OD⊥BC,OE⊥AC,
∴D,E分别是线段BC,AC的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AB=$\frac{5\sqrt{2}}{2}$.连结OC.
∵OD⊥BC,OE⊥AC,OB=OC=OA,
∴∠BOD=∠COD,∠AOE=∠COE.
∵∠AOB=90°,
∴∠DOE=∠COD+∠COE=$\frac{1}{2}$∠AOB=45°.
查看更多完整答案,请扫码查看


