8. 如图,$AB$是$\odot O$的直径,$CD$是弦,点$C$,$D$在直径$AB$的两侧.若$\angle AOC:\angle AOD:\angle DOB = 2:7:11$,$CD = 4$,则$\overset{\frown}{CD}$的长为(

A.$2\pi$
B.$4\pi$
C.$\frac{\sqrt{2}}{2}\pi$
D.$\sqrt{2}\pi$
D
)
A.$2\pi$
B.$4\pi$
C.$\frac{\sqrt{2}}{2}\pi$
D.$\sqrt{2}\pi$
答案:
8.D
9. 如图,已知$\triangle ABC$是$\odot O$的内接三角形,$AD$是$\odot O$的直径,连结$BD$,$BC$平分$\angle ABD$.
(1) 求证:$\angle CAD = \angle ABC$.
(2) 若$AD = 6$,求$\overset{\frown}{CD}$的长.
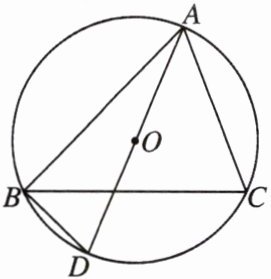
(1) 求证:$\angle CAD = \angle ABC$.
(2) 若$AD = 6$,求$\overset{\frown}{CD}$的长.

答案:
9.解:
(1)
∵$BC$平分$\angle ABD$,$\therefore\angle DBC = \angle ABC$,
∵$\angle CAD = \angle DBC$,$\therefore\angle CAD = \angle ABC$.
(2)
∵$\angle CAD = \angle ABC$,$\therefore\widehat{CD}=\widehat{AC}$,
∵$AD$是$\odot O$的直径,
$AD = 6$,$\therefore\widehat{CD}$的长$=\frac{1}{2}×\frac{1}{2}×\pi×6=\frac{3}{2}\pi$.
(1)
∵$BC$平分$\angle ABD$,$\therefore\angle DBC = \angle ABC$,
∵$\angle CAD = \angle DBC$,$\therefore\angle CAD = \angle ABC$.
(2)
∵$\angle CAD = \angle ABC$,$\therefore\widehat{CD}=\widehat{AC}$,
∵$AD$是$\odot O$的直径,
$AD = 6$,$\therefore\widehat{CD}$的长$=\frac{1}{2}×\frac{1}{2}×\pi×6=\frac{3}{2}\pi$.
10. 如图,在矩形$ABCD$中,点$F$在边$BC$上,且$AF = AD$,过点$D$作$DE\perp AF$,垂足为$E$.
(1) 求证:$DE = AB$.
(2) 以$D$为圆心、$DE$为半径作圆弧交$AD$于点$G$.若$BF = FC = 1$,试求$\overset{\frown}{EG}$的长.
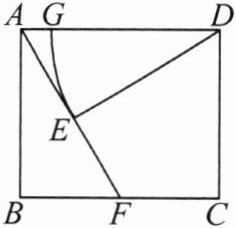
(1) 求证:$DE = AB$.
(2) 以$D$为圆心、$DE$为半径作圆弧交$AD$于点$G$.若$BF = FC = 1$,试求$\overset{\frown}{EG}$的长.

答案:
10.解:
(1)证明:
∵$DE\perp AF$,$\therefore\angle AED = 90^{\circ}$.
又
∵四边形$ABCD$是矩形,$\therefore AD// BC$,$\angle B = 90^{\circ}$.
$\therefore\angle DAE = \angle AFB$,$\angle AED = \angle B = 90^{\circ}$.
又
∵$AF = AD$,$\therefore\triangle ADE\cong\triangle FAB(AAS)$,$\therefore DE = AB$.
(2)
∵$BF = FC = 1$,$\therefore AD = BC = BF + FC = 2$.
又
∵$\triangle ADE\cong\triangle FAB$,$\therefore AE = BF = 1$.
$\therefore$在$Rt\triangle ADE$中,$AE=\frac{1}{2}AD$,$\therefore\angle ADE = 30^{\circ}$.
又
∵$DE = \sqrt{AD^{2}-AE^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
$\therefore\widehat{EG}=\frac{n\pi R}{180}=\frac{30\cdot\pi\cdot\sqrt{3}}{180}=\frac{\sqrt{3}}{6}\pi$.
(1)证明:
∵$DE\perp AF$,$\therefore\angle AED = 90^{\circ}$.
又
∵四边形$ABCD$是矩形,$\therefore AD// BC$,$\angle B = 90^{\circ}$.
$\therefore\angle DAE = \angle AFB$,$\angle AED = \angle B = 90^{\circ}$.
又
∵$AF = AD$,$\therefore\triangle ADE\cong\triangle FAB(AAS)$,$\therefore DE = AB$.
(2)
∵$BF = FC = 1$,$\therefore AD = BC = BF + FC = 2$.
又
∵$\triangle ADE\cong\triangle FAB$,$\therefore AE = BF = 1$.
$\therefore$在$Rt\triangle ADE$中,$AE=\frac{1}{2}AD$,$\therefore\angle ADE = 30^{\circ}$.
又
∵$DE = \sqrt{AD^{2}-AE^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$,
$\therefore\widehat{EG}=\frac{n\pi R}{180}=\frac{30\cdot\pi\cdot\sqrt{3}}{180}=\frac{\sqrt{3}}{6}\pi$.
查看更多完整答案,请扫码查看


