《2025年名师面对面学科素养评价九年级数学全一册浙教版》

7. 如果函数$y=(k - 2)x^{k^{2}-2k + 2}+kx + 1$是关于$x$的二次函数，那么$k$的值是(D)

A.$1$或$2$
B.$0$或$2$
C.$2$
D.$0$

答案： 7.D

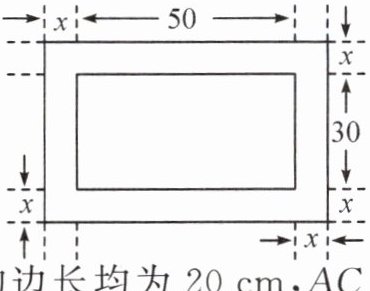
8. 如图所示，在一幅长$50cm$、宽$30cm$的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂画.设整个挂画总面积为$y(cm^{2})$，金色纸边的宽为$x(cm)$，则$y$与$x$的函数表达式是y = 4x^{2}+160x + 1500.

答案： $8.y = 4x^{2}+160x + 1500$

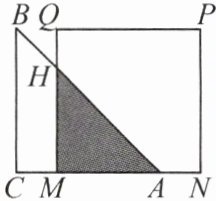
9. 如图，已知等腰直角三角形$ABC$的直角边长与正方形$MNPQ$的边长均为$20cm$，$AC$与$MN$在同一条直线上.开始时点$A$与点$N$重合，$\triangle ABC$以$2cm/s$的速度向左运动，最终点$A$与点$M$重合.
（1）求重叠部分的面积$y(cm^{2})$与时间$t(s)$之间的函数表达式和自变量的取值范围.
（2）当$t = 1s$，$t = 2s$时，求重叠部分的面积.

答案： 9.解：$(1)\because\triangle ABC$是等腰直角三角形，
$\therefore$重叠部分也是等腰直角三角形.
又$\because AN = 2t,\therefore AM = MN - AN = 20 - 2t，$
$\therefore MH = AM = 20 - 2t，$
$\therefore$重叠部分的面积为$y=\frac{1}{2}(20 - 2t)^{2}=2t^{2}-40t + 200.$
自变量的取值范围是$0\leqslant t\leqslant10.$
(2)当t = 1时，y = 162;当t = 2时，y = 128.当t = 1时，重叠部分的面积为$162cm^{2}，$t = 2时，重叠部分的面积为$128cm^{2}.$

10. 某公司生产的$A$种产品，每件成本是$2$元，每件售价是$3$元，一年的销售量是$10$万件.为了获得更多的利润，公司准备拿出一定资金来做广告.根据经验，每年投入的广告费为$x$（万元）时，产品的年销售量是原来的$y$倍，且$y$是$x$的二次函数.公司作了预测，已知$x$与$y$之间的对应关系如下表：

（1）根据上表，求$y$关于$x$的函数表达式.
（2）如果把利润看成是销售总额减去成本和广告费，请你写出年利润$S$（万元）与广告费$x$（万元）的函数表达式.

答案： 10.解：
(1)设所求函数表达式为$y = ax^{2}+bx + c，$
把(0,1),(1,1.5),(2,1.8)分别代入上式，
得$\begin{cases}1 = c,\\1.5 = a + b + c,\\1.8 = 4a + 2b + c,\end{cases}$
解得$a = -\frac{1}{10},b = \frac{3}{5},c = 1,\therefore y = -\frac{1}{10}x^{2}+\frac{3}{5}x + 1.$
$(2)S=(3 - 2)×10y - x=(-\frac{1}{10}x^{2}+\frac{3}{5}x + 1)×10 - x=$
$-x^{2}+5x + 10.$