7. 如图,$ MN $是$ \odot O $的直径,点$ A $是半圆上一个三等分点,点$ B $是$ \overset{\frown}{AN} $的中点,点$ B' $是点$ B $关于$ MN $的对称点,$ \odot O $的半径为$ 1 $,则$ AB' $的长等于(

A.1
B.$ \sqrt{2} $
C.$ \sqrt{3} $
D.2
B
)
A.1
B.$ \sqrt{2} $
C.$ \sqrt{3} $
D.2
答案:
7.B
8. 在直径为$ 10 $的$ \odot O $中,弦$ AB = 5 $,$ BC = 5\sqrt{2} $,则$ \angle ABC $的度数是
15°或105°
.
答案:
8.15°或105°
9. 如图,$ AB $是圆$ O $的弦,$ C $,$ D $是$ AB $上两点,$ AC = BD $,求证:$ \overset{\frown}{AF} = \overset{\frown}{BE} $.
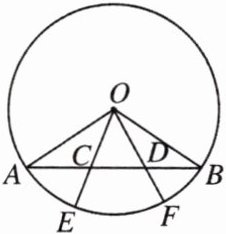

答案:
9.证明:
∵OA=OB,
∴∠A=∠B,在△OAC和△OBD中,
$\begin{cases} OA = OB, \\ ∠A = ∠B, \\ AC = BD, \end{cases}$
∴△OAC≌△OBD,
∴∠AOE=∠BOF,
AE = BF,
∴$\overset{\frown}{AF} = \overset{\frown}{BE}$.
∵OA=OB,
∴∠A=∠B,在△OAC和△OBD中,
$\begin{cases} OA = OB, \\ ∠A = ∠B, \\ AC = BD, \end{cases}$
∴△OAC≌△OBD,
∴∠AOE=∠BOF,
AE = BF,
∴$\overset{\frown}{AF} = \overset{\frown}{BE}$.
10. 如图,$ AB $为$ \odot O $的直径,$ C $,$ D $分别为$ OA $,$ OB $的中点,$ CF \perp AB $,$ ED \perp AB $,点$ E $,$ F $都在$ \odot O $上,求证:
(1)$ CF = DE $.
(2)$ \overset{\frown}{AF} = \overset{\frown}{EF} = \overset{\frown}{BE} $.
(3)$ AE = 2CF $.
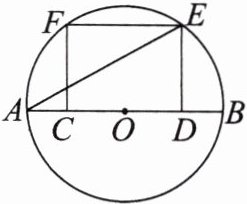
(1)$ CF = DE $.
(2)$ \overset{\frown}{AF} = \overset{\frown}{EF} = \overset{\frown}{BE} $.
(3)$ AE = 2CF $.

答案:
10.证明:
(1)连结OF,OE,如图,
∵AB为⊙O的直径,C,D分别为OA, OB的中点,
OB的中点,
∴OC=OD,而OF=OE,
∴Rt△OCF≌Rt△ODE,
∴CF=DE.
(2)在Rt△OCF中,OC=$\frac{1}{2}$OF,
∴∠CFO=30°,
∴∠COF=60°,同理∠BOE=60°,
∴∠EOF=60°,
∴∠AOF=∠FOE=∠EOD,
∴$\overset{\frown}{AF} = \overset{\frown}{EF} = \overset{\frown}{BE}$.
(3)
∵OE=OA,
∴∠A=∠OEA,
∵∠DOE=∠A+∠OEA=60°,
∴∠A=30°,
∴AE=2DE,
∴AE=2CF.
10.证明:
(1)连结OF,OE,如图,
∵AB为⊙O的直径,C,D分别为OA,
 OB的中点,
OB的中点,∴OC=OD,而OF=OE,
∴Rt△OCF≌Rt△ODE,
∴CF=DE.
(2)在Rt△OCF中,OC=$\frac{1}{2}$OF,
∴∠CFO=30°,
∴∠COF=60°,同理∠BOE=60°,
∴∠EOF=60°,
∴∠AOF=∠FOE=∠EOD,
∴$\overset{\frown}{AF} = \overset{\frown}{EF} = \overset{\frown}{BE}$.
(3)
∵OE=OA,
∴∠A=∠OEA,
∵∠DOE=∠A+∠OEA=60°,
∴∠A=30°,
∴AE=2DE,
∴AE=2CF.
查看更多完整答案,请扫码查看


