《2025年名师面对面学科素养评价九年级数学全一册浙教版》

6. 如图，王华晚上由路灯 $ A $ 下的 $ B $ 处走到 $ C $ 处时，测得影子 $ CD $ 的长为 $ 1 $ 米，继续往前走 $ 3 $ 米到达 $ E $ 处时，测得影子 $ EF $ 的长为 $ 2 $ 米。已知王华的身高是 $ 1.5 $ 米，那么路灯 $ A $ 的高度 $ AB $ 等于(B)

A.$ 4.5 $ 米
B.$ 6 $ 米
C.$ 7.2 $ 米
D.$ 8 $ 米

答案： 6.B

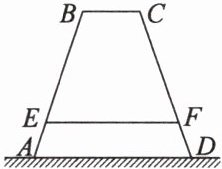
7. 某高中学校为高一新生设计的学生板凳的正面示意图如图所示，其中 $ BA = CD $，$ BC = 20 cm $，$ BC $，$ EF $ 平行于地面 $ AD $ 且到地面 $ AD $ 的距离分别为 $ 40 cm $，$ 8 cm $。为使板凳两腿底端 $ A $，$ D $ 之间的距离为 $ 50 cm $，那么横梁 $ EF $ 应为多长？（材质及其厚度等忽略不计）

答案： 7.解:过点C作CM//AB，交EF，AD于N,M,作CP⊥AD，交EF,AD于Q,P.
　由题意，得四边形ABCM是平行四边形，
∴EN=AM=BC=20(cm)，
∴MD=AD−AM=50−20=30(cm).
　由题意知CP=40cm，PQ=8cm，
∴CQ=32cm，
∵EF//AD，
∴△CNF∽△CMD，
∴$\frac{NF}{MD} = \frac{CQ}{CP}$，即$\frac{NF}{30} = \frac{32}{40}$.解得NF=24(cm)，
∴EF=EN+NF=20+24=44(cm)，
答:横梁EF应为44cm.

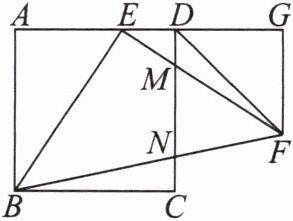
8. 如图，四边形 $ ABCD $ 是正方形，点 $ E $ 在边 $ AD $ 上，$\triangle BEF $ 是以 $ E $ 为直角顶点的等腰直角三角形。$ EF $，$ BF $ 分别交 $ CD $ 于点 $ M $，$ N $，过点 $ F $ 作 $ AD $ 的垂线交 $ AD $ 的延长线于点 $ G $，连结 $ DF $。请完成下列问题：
（1）求 $ \angle FDG $ 的度数。
（2）若 $ DE = 1 $，$ DF = 2\sqrt{2} $，求线段 $ MN $ 的长度。

答案：
8.解:
(1)易证△ABE≌△GEF(AAS)，
∴EG=AB=AD，GF =AE，
　即DG+DE=AE+DE，
∴DG=AE，
∴DG=GF，即△DGF 是等腰直角三角形，
∴∠FDG=45°.
(2)
∵DE=1，DF=$2\sqrt{2}$，
∴DG=GF =2，AB=AD=CD=ED+DG=2+1=3，延长GF交BC延长线于点H，
∴CD//GH，
∴△EDM∽△EGF，
∴$\frac{MD}{GF} = \frac{ED}{EG}$，即$\frac{MD}{2} = \frac{1}{3}$，
∴MD=$\frac{2}{3}$，同理△BNC∽△BFH，
∴$\frac{NC}{FH} = \frac{BC}{BH}$，
　即$\frac{NC}{GH - GF} = \frac{BC}{BC + CH}$，
∴$\frac{NC}{3 - 2} = \frac{3}{3 + 2}$，
∴NC=$\frac{3}{5}$，
∴MN=CD−MD−NC=3−$\frac{2}{3}$−$\frac{3}{5}$=$\frac{26}{15}$.