《2025年名师面对面学科素养评价九年级数学全一册浙教版》

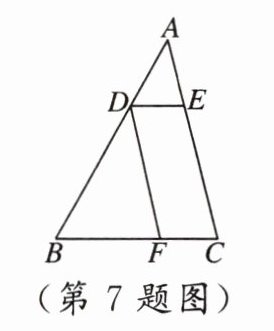
7. 如图，点$D$，$E$，$F$分别在$\triangle ABC$的各边上，且$DE// BC$，$DF// AC$。若$AE:EC = 1:2$，$BF = 6$，则$DE$的长为(C)

A.$1$
B.$2$
C.$3$
D.$4$

答案： 7.C

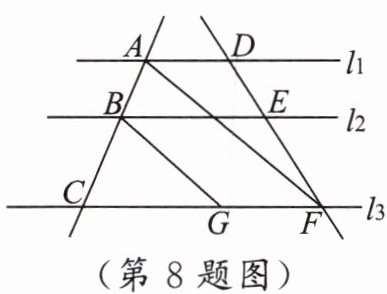
8. 如图，直线$l_1// l_2// l_3$，直线$AC$，$DF$分别交$l_1$，$l_2$，$l_3$于点$A$，$B$，$C$和点$D$，$E$，$F$，连结$AF$，作$BG// AF$。若$\frac{DE}{EF}=\frac{2}{3}$，$BG = 6$，则$AF$的长为(C)

A.$8$
B.$9$
C.$10$
D.$11$

答案： 8.C

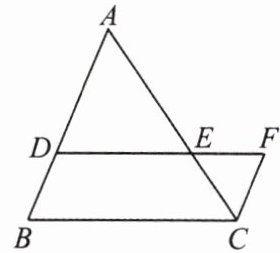
9. 如图，已知$\triangle ABC$中，点$D$，$E$分别在边$AB$和$AC$上，$DE// BC$，点$F$是$DE$延长线上的点，$\frac{AD}{BD}=\frac{DE}{EF}$，连结$FC$。若$\frac{AE}{AC}=\frac{2}{3}$，求$\frac{AD}{FC}$的值。

答案： 9.解:
∵DE//BC,
∴$\frac{AD}{BD}$=$\frac{AE}{EC}$.
　又
∵$\frac{AD}{BD}$=$\frac{DE}{EF}$,
∴$\frac{AE}{EC}$=$\frac{DE}{EF}$,
∴AB//CF.
∴$\frac{AD}{FC}$=$\frac{AE}{EC}$.
∵$\frac{AE}{AC}$=$\frac{2}{3}$,$\therefore \frac{AE}{EC}=\frac{2}{1}=2$,$\therefore \frac{AD}{FC}=2$.

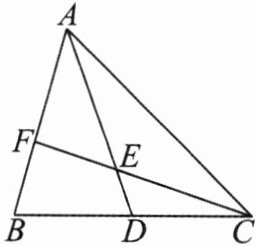
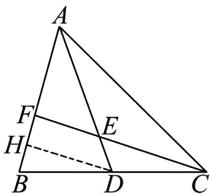
10. 在$\triangle ABC$中，$AD$为$BC$上的中线，点$E$在$AD$上，且$\frac{DE}{AE}=\frac{1}{3}$，射线$CE$交$AB$于点$F$，求$\frac{AF}{FB}$的值。

答案：
10.解:过点D作DH//FC交AB于H，则
　$\frac{FH}{AF}$=$\frac{DE}{AE}$=$\frac{1}{3}$,$\frac{FH}{HB}$=$\frac{CD}{BD}$=1,
　
∴$\frac{AF}{FB}$=$\frac{3}{2}$.