2025年点对点期末复习及智胜暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年点对点期末复习及智胜暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
13. 如图,$△ADB是由△AEC绕点A沿顺时针旋转44^{\circ}$得到的,则$∠ABC= $

$68^{\circ}$

答案:
$68^{\circ}$
14. 如图,已知$AB// OC$,$CD// OA$,$∠3 = ∠4$,$∠1 = 30^{\circ}$,则$∠2$的度数为____

$30^{\circ}$

答案:
$30^{\circ}$
15. 某单位组建一支$25×25$的方队参加“唱红歌,念党恩”七一文艺汇演,如表反映的是该方队队员的年龄情况:
|年龄(岁)|18|19|20|21|22|
|人数(人)|94|128|183|157|63|
则这625名队员年龄的平均数、众数、中位数中最大的是
|年龄(岁)|18|19|20|21|22|
|人数(人)|94|128|183|157|63|
则这625名队员年龄的平均数、众数、中位数中最大的是
众数和中位数
。
答案:
众数和中位数
16. 如图所示,是某超市自动扶梯的示意图,大厅两层之间的距离$h = 6.5$米,自动扶梯的倾角为$30^{\circ}$,若自动扶梯运行速度为$v = 0.5$米/秒,则顾客乘自动扶梯上一层楼的时间为
26
秒.
答案:
26
17. 如图,某公司在门前长方形小广场$ABCD$上空放一氢气球,为使氢气球悬挂于广场中央$F$的正上方,公司欲从点$A到气球E$拉一根细绳,已知小广场宽$AB = 18$米,$BC = 24$米,气球高$EF = 8$米,则细绳$AE$的长为____
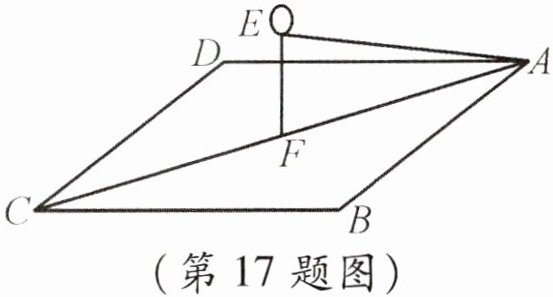
17 米
。
答案:
17 米
18. 某工厂去年的利润为200万元,今年的总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元,则去年的总产值为
2000 万元
。
答案:
2000 万元
19. 某中学七、八、九年级共有学生620名,将这些学生按年龄分组,$13\sim 15$岁这一组的频率为0.3,那么估计$13\sim 15$岁范围内的学生有
186
名.
答案:
186
20. 现在我们定义一种运算的新方法“$\odot$”:$a\odot b = (a + b)(a - b)$,则以此方法将式子$(x\odot y)\odot x^{2}$化简为
$y^{4} - 2x^{2}y^{2}$
。
答案:
$y^{4} - 2x^{2}y^{2}$
21. (6分)已知$\begin{cases}3a + 2b = 13\\2a + 3b = 12\end{cases} $,求$(a + b)^{2}+(a - b)^{2024}$的值.
解:$\begin{cases}3a + 2b = 13①\\2a + 3b = 12②\end{cases}$,
$① + ②$,得$5(a + b) = 25$,则$a + b = $
$① - ②$,得$a - b = $
$\therefore$ 原式$= $
解:$\begin{cases}3a + 2b = 13①\\2a + 3b = 12②\end{cases}$,
$① + ②$,得$5(a + b) = 25$,则$a + b = $
5
,$① - ②$,得$a - b = $
1
,$\therefore$ 原式$= $
5
$^{2} + $1
$^{2024} = 25 + 1 = $26
。
答案:
解:$\begin{cases}3a + 2b = 13①\\2a + 3b = 12②\end{cases}$,
$① + ②$,得$5(a + b) = 25$,则$a + b = 5$,
$① - ②$,得$a - b = 1$,
$\therefore$ 原式$= 5^{2} + 1^{2024} = 25 + 1 = 26$。
$① + ②$,得$5(a + b) = 25$,则$a + b = 5$,
$① - ②$,得$a - b = 1$,
$\therefore$ 原式$= 5^{2} + 1^{2024} = 25 + 1 = 26$。
22. (6分)在一次军事演习中,红方原计划要从$A$地向距离150千米的$B$地的蓝方发起攻击.为了迷惑蓝方,红方先向蓝方另一支部队所在的$C$地前进,当蓝方从$B地向C$地增援后,红方突然转向,向$B$地进发,拿下了$B$地.这样红方比原计划多行进90千米,而且行进速度是原计划
的
$\frac{4}{3}$倍,但比原计划晚1小时到达$B$地.试求红方实际行进速度.
答案:
解:设红方原计划行进速度为$x$千米/时,
由题意得$\frac{150 + 90}{\frac{4}{3}x} - \frac{150}{x} = 1$,
解得$x = 30$,
经检验,$x = 30$是原方程的解,且符合题意,
当$x = 30$时,$\frac{4}{3}x = 40$千米/时,
答:红方实际行进速度为 40 千米/时。
由题意得$\frac{150 + 90}{\frac{4}{3}x} - \frac{150}{x} = 1$,
解得$x = 30$,
经检验,$x = 30$是原方程的解,且符合题意,
当$x = 30$时,$\frac{4}{3}x = 40$千米/时,
答:红方实际行进速度为 40 千米/时。
查看更多完整答案,请扫码查看


