2025年点对点期末复习及智胜暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年点对点期末复习及智胜暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
(2)某工厂现有甲种原料226kg,乙种原料250kg,计划利用这两种原料生产$A$、$B$两种产品共40件,生产$A$、$B$两种产品用料情况如表:
| |需要用甲原料|需要用乙原料|
|一件$A$产品|7kg|4kg|
|一件$B$产品|3kg|10kg|
若设生产$A产品x$件,求$x$的值,并说明有哪几种符合题意的生产方案。
| |需要用甲原料|需要用乙原料|
|一件$A$产品|7kg|4kg|
|一件$B$产品|3kg|10kg|
若设生产$A产品x$件,求$x$的值,并说明有哪几种符合题意的生产方案。
答案:
【解析】:设生产$A$产品$x$件,则生产$B$产品$(40 - x)$件。根据甲种原料不超过$226kg$,可得$7x + 3(40 - x) \leq 226$;根据乙种原料不超过$250kg$,可得$4x + 10(40 - x) \leq 250$。解第一个不等式:$7x + 120 - 3x \leq 226$,$4x \leq 106$,$x \leq 26.5$。解第二个不等式:$4x + 400 - 10x \leq 250$,$-6x \leq -150$,$x \geq 25$。所以$x$的取值范围是$25 \leq x \leq 26.5$,因为$x$为正整数,所以$x = 25$或$26$。当$x = 25$时,$40 - x = 15$;当$x = 26$时,$40 - x = 14$。
【答案】:$x$的值为25或26,共有2种符合题意的生产方案,方案1:生产$A$产品25件,$B$产品15件;方案2:生产$A$产品26件,$B$产品14件。
【答案】:$x$的值为25或26,共有2种符合题意的生产方案,方案1:生产$A$产品25件,$B$产品15件;方案2:生产$A$产品26件,$B$产品14件。
9. 某超市销售甲、乙两种商品,甲商品每件进价10元,售价15元;乙商品每件进价30元,售价40元。
(1)若该超市同时一次购进甲、乙两种商品共80件,恰好用去1600元,求购进甲、乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
(1)若该超市同时一次购进甲、乙两种商品共80件,恰好用去1600元,求购进甲、乙两种商品各多少件?
(2)该超市为使甲、乙两种商品共80件的总利润不少于600元,但又不超过610元,请你帮助该超市设计相应的进货方案。
答案:
解:
(1) 设购进甲种商品 $a$ 件,则购进乙种商品 $(80 - a)$ 件,
依题意得:$10a + 30(80 - a) = 1600$,解得:$a = 40$,
∴ $80 - a = 40$,
答:购进甲种商品 40 件,购进乙种商品 40 件;
(2) 设购进甲种商品 $x$ 件,则购进乙种商品 $(80 - x)$ 件,
依题意可得:$\begin{cases}(15 - 10)x + (40 - 30)(80 - x) \geq 600\\(15 - 10)x + (40 - 30)(80 - x) \leq 610\end{cases}$,
解得:$38 \leq x \leq 40$,
∵ $x$ 为整数,
∴ $x = 38, 39, 40$,
故有三种进货方案:
方案一:购进甲种商品 38 件,乙种商品 42 件;
方案二:购进甲种商品 39 件,乙种商品 41 件;
方案三:购进甲种商品 40 件,乙种商品 40 件。
(1) 设购进甲种商品 $a$ 件,则购进乙种商品 $(80 - a)$ 件,
依题意得:$10a + 30(80 - a) = 1600$,解得:$a = 40$,
∴ $80 - a = 40$,
答:购进甲种商品 40 件,购进乙种商品 40 件;
(2) 设购进甲种商品 $x$ 件,则购进乙种商品 $(80 - x)$ 件,
依题意可得:$\begin{cases}(15 - 10)x + (40 - 30)(80 - x) \geq 600\\(15 - 10)x + (40 - 30)(80 - x) \leq 610\end{cases}$,
解得:$38 \leq x \leq 40$,
∵ $x$ 为整数,
∴ $x = 38, 39, 40$,
故有三种进货方案:
方案一:购进甲种商品 38 件,乙种商品 42 件;
方案二:购进甲种商品 39 件,乙种商品 41 件;
方案三:购进甲种商品 40 件,乙种商品 40 件。
例1 学校组织同学们春游,租用45座和30座两种型号的客车,若租用45座客车$x$辆,租用30座客车$y$辆,则不等式“$45x + 30y ≥ 500$”表示的实际意义是(
A.两种客车总的载客量不少于500人
B.两种客车总的载客量不超过500人
C.两种客车总的载客量不足500人
D.两种客车总的载客量超过500人
A
)A.两种客车总的载客量不少于500人
B.两种客车总的载客量不超过500人
C.两种客车总的载客量不足500人
D.两种客车总的载客量超过500人
答案:
A
1. 用适当的不等式表示下列关系:
(1)$a$是非负数:
(2)$x$与2的差不足15:
(1)$a$是非负数:
$a \geq 0$
;(2)$x$与2的差不足15:
$x - 2 < 15$
。
答案:
(1) $a \geq 0$;
(2) $x - 2 < 15$
(1) $a \geq 0$;
(2) $x - 2 < 15$
2. 按商品质量规定:商店出售的标明500g的袋装食盐,其实际克数与所标克数相差不能超过5g,设实际克数是$xg$,则$x$应满足的条件是
$495 \leq x \leq 505$
。
答案:
$495 \leq x \leq 505$
例2 解不等式:$3x - 2 > πx + 5$。
答案:
【解析】:解不等式$3x - 2 > πx + 5$,首先移项可得$3x - πx > 5 + 2$,合并同类项得$(3 - π)x > 7$。因为$3 - π$是负数($π\approx3.14$,所以$3 - π\lt0$),根据不等式的性质,当不等式两边同时除以一个负数时,不等号的方向需要改变,所以系数化为1得$x < \frac{7}{3 - π}$。
【答案】:$x < \frac{7}{3 - π}$
【答案】:$x < \frac{7}{3 - π}$
3. 若$x > y$,则下列式子错误的是(
A.$x - 3 > y - 3$
B.$-3x > -3y$
C.$x + 3 > y + 3$
D.$\frac{x}{3} > \frac{y}{3}$
B
)A.$x - 3 > y - 3$
B.$-3x > -3y$
C.$x + 3 > y + 3$
D.$\frac{x}{3} > \frac{y}{3}$
答案:
B
4. 已知$x > y$,若对任意实数$a$,有下列结论:①$ax > ay$;②$a^2 - x > a^2 - y$;③$a^2 + x ≤ a^2 + y$;④$a^2x ≥ a^2y$,其中正确的是(
A.①
B.②
C.③
D.④
D
)A.①
B.②
C.③
D.④
答案:
D
例3 下列四个不等式组:$-3 < x < 2$;$-3 ≤ x < 2$;$-3 < x ≤ 2$;$-3 ≤ x ≤ 2$,其中一个不等式组的解集在数轴上的正确表示如图所示,这个不等式组是
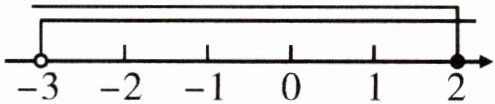
$-3 < x ≤ 2$
。
答案:
$-3 < x ≤ 2$
查看更多完整答案,请扫码查看


