《2025年点对点期末复习及智胜暑假八年级数学北师大版》

19. 已知多项式$x^{2}+y^{2}-6x+4y+20$,它的最小值是7,此时$x= $3,$y= $-2.

答案： 7 3 -2

20. 如图,在直角坐标系中,AC是$Rt△OAB$的角平分线,点C到AB的距离是5,则点C的坐标是____(-5,0).

答案： (-5,0)

21. 已知关于x的一元一次不等式组$\left\{\begin{array}{l} \frac {x+21}{2}＞3-x\\ x＜m\end{array} \right. $的所有整数解的和是-7,则m的取值范围是-3 ＜ m ≤ -2 或 2 ＜ m ≤ 3.

答案： -3 ＜ m ≤ -2 或 2 ＜ m ≤ 3

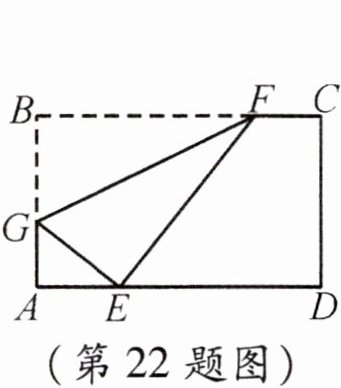
22. 如图,折叠矩形纸片ABCD,使点B落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且$AB= 6,BC= 10$.设$AE= x$,则x的取值范围是2 ≤ x ≤ 6.

答案： 2 ≤ x ≤ 6

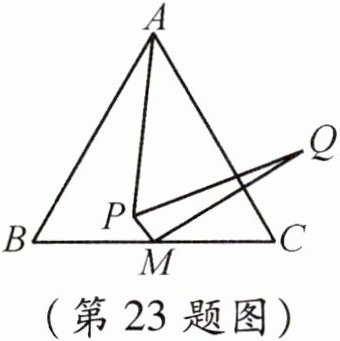
23. 如图,等边$△ABC$中,$BC= 16$,M为BC的中点,P为$△ABC$内一动点,$PM= 2$,连接AP,将线段AP绕点P顺时针旋转$60^{\circ }$得PQ,连接MQ,则线段MQ长度的最小值为____8√3 - 2.

答案： 8√3 - 2

24. 某商店销售A、B两种型号的电脑,销售一台B型电脑的利润比销售一台A型电脑的利润多50元.已知销售相同数量的A、B两种型号的电脑分别获利1000元和1500元.
(1)求每台A型电脑和B型电脑的销售利润；
(2)该商店计划一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍.设购进A型电脑n台,这100台电脑的销售总利润为w元.
①直接写出w与n之间的函数关系式为____w=-50n+15000(34≤n≤100，且n为整数)；
②该商店购进A型、B型电脑各多少台,才能使销售利润最大？最大利润是多少？

答案：
(1)设每台A型电脑的销售利润为x元，则每台B型电脑的销售利润为(x + 50)元，
根据题意得：$\frac{1000}{x}=\frac{1500}{x + 50}$，解得x = 100，
经检验，x = 100是原方程的解，且符合题意，
∴x + 50 = 150元，
答：每台A型电脑的销售利润为100元，每台B型电脑的销售利润为150元；
(2)①w = -50n + 15000($\frac{100}{3}$ ≤ n ≤ 100，且n为整数)；
②
∵w = -50n + 15000中，-50 ＜ 0，
∴w随n的增大而减小，
∵$\frac{100}{3}$ ≤ n ≤ 100且n为整数，
∴当n = 34时，w取最大值，最大值为-50 × 34 + 15000 = 13300，此时100 - n = 100 - 34 = 66台，
答：商店购进A型电脑34台，B型电脑66台，才能使销售利润最大，最大利润是13300元。

25. 如图,在平面直角坐标系xOy中,将含$30^{\circ }$角的直角三角板ABC的顶点A放置在点$(-2,4)$,较长的直角边$AB= 3\sqrt {3}$,AB所在直线与x轴所成锐角为$60^{\circ }$.将直角三角板ABC沿AB翻折,点C的对应点为点P.
(1)求点C的坐标；
(2)在x轴上存在点Q,使得$△BPQ$的面积为3,求点Q的坐标；
(3)已知点M是直线CB上的一动点,点N是直线AB上的一动点,点E是平面上的一点,是否存在四边形CMEN为菱形,且$∠CNE= 120^{\circ }$?若存在,求出菱形CMEN的面积；若不存在,请说明理由.

答案：
解：
(1)如图1，设AC与x轴交于H，直线AB交x轴于F，
由题意得：∠AFH = 60°，
∵∠BAC = 30°，
∴∠AHF = 90°，
在Rt△ABC中，
AB = 3√3，∠CAB = 30°，设BC = a，则AC = 2a，
∴(2a)² - a² = (3√3)²，
解得a₁ = 3，a₂ = -3(舍去)，
∴AC = 2a = 6，
∵A(-2,4)，
∴AH = 4，
∴CH = 2，
∴C(-2,-2)；

(2)当Q在PB的右侧时，
如图2，设AC交x轴于H，CP交x轴于T，作Q₁G⊥直线PB于G，
由
(1)得BC = 3，
∴PB = BC = 3，
∵S_{△BPQ} = 3，
∴$\frac{1}{2}$ × 3GQ₁ = 3，
∴GQ₁ = 2，
在Rt△TGQ₁中，GQ₁ = 2，∠GTQ₁ = 30°，
∴TQ₁ = 2GQ₁ = 4，
在Rt△CTH中，CH = 2，∠HTC = 30°，
∴CT = 2CH = 4，
∴HT = √{CT² - CH²} = √{4² - 2²} = 2√3，
∴OT = HT - OH = 2√3 - 2，
∴OQ₁ = OT + TQ₁ = 2√3 + 2，
∴Q₁(2√3 + 2,0)；
同理，当Q在PB的左侧时，Q₂(2√3 - 6,0)，
综上所述，点Q的坐标为(2√3 + 2,0)或(2√3 - 6,0)；
(3)存在，
①当点M与点P重合时，
如图3，作出菱形CMEN，
∵∠BAC = 30°，∠ABC = 90°，
∴∠ACM = °60，
在菱形CMEN中，CM // NE，
∴∠CNE = 120°；

②当点M与点P重合，点N与点A关于PC的对称点重合时，
如图3，作出菱形CME'N'，
易知四边形ACN'P是菱形，
∴∠N'CP = ∠ACP = 60°，
在菱形CME'N'中CM // N'E'，
∴∠CN'E' = 120°，
综上所述，存在四边形CMEN为菱形，且∠CNE = 120°；
∴S_{菱形CMEN} = 2S_{△ACP} =４S_{△ABC} = 4 × $\frac{1}{2}$AB · BC = 4 × $\frac{1}{2}$ × 3√3 × 3 = 18√3。