2025年点对点期末复习及智胜暑假八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年点对点期末复习及智胜暑假八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
4. 如图是一个旋转对称图形,要使它旋转后与自身重合,至少应将它绕中心逆时针方向旋转的度数为(
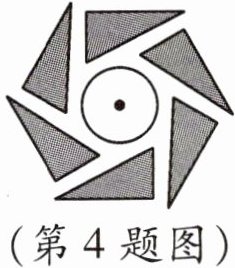
A.30°
B.60°
C.120°
D.180°
B
)
A.30°
B.60°
C.120°
D.180°
答案:
B
5. 下列各图中,能由“基本图案”通过旋转变换得到的图形是(

A
)
答案:
A
6. 下列图形中,必须由“基本图形”既平移又旋转而形成的图形是(
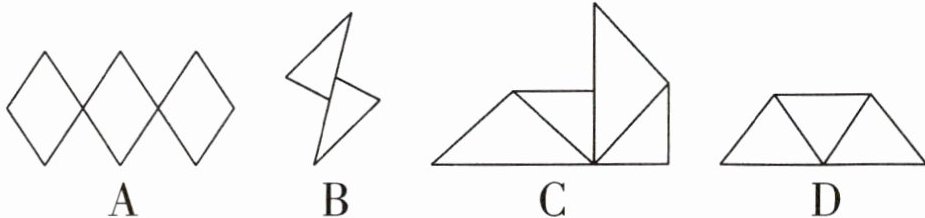
D
)
答案:
D
7. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接AA',若∠1 = 25°,则∠BAA'的度数是(

A.55°
B.60°
C.65°
D.70°
C
)
A.55°
B.60°
C.65°
D.70°
答案:
C
8. 如图,是用围棋子摆出的图案(棋子的位置用有序数对表示,如:点A在(5,1)的位置)。若再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是(

A.黑(3,3),白(3,1)
B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5)
D.黑(3,2),白(3,3)
B
)
A.黑(3,3),白(3,1)
B.黑(3,1),白(3,3)
C.黑(1,5),白(5,5)
D.黑(3,2),白(3,3)
答案:
B
9. 如图,△DEF是由△ABC通过平移得到的,且点B,E,C,F在同一条直线上。若BF = 14,EC = 6,则BE的长度是______

4
。
答案:
解:
∵△DEF是由△ABC平移得到的,
∴BC=EF,
∵BC=BE+EC,EF=EC+CF,
∴BE=CF,
∵BF=BE+EC+CF=14,EC=6,
∴BE+CF=14-6=8,
∵BE=CF,
∴BE=8÷2=4。
4
∵△DEF是由△ABC平移得到的,
∴BC=EF,
∵BC=BE+EC,EF=EC+CF,
∴BE=CF,
∵BF=BE+EC+CF=14,EC=6,
∴BE+CF=14-6=8,
∵BE=CF,
∴BE=8÷2=4。
4
10. 如图是一个以点A为对称中心的中心对称图形,若∠C = 90°,∠B = 30°,AC = 1,则BB'的长为______

4
。
答案:
解:在Rt△ABC中,∠C=90°,∠B=30°,AC=1,
∵∠B=30°,
∴AB=2AC=2×1=2,
∵图形是以点A为对称中心的中心对称图形,
∴AB=AB',
∴BB'=AB+AB'=2+2=4。
故答案为:4。
∵∠B=30°,
∴AB=2AC=2×1=2,
∵图形是以点A为对称中心的中心对称图形,
∴AB=AB',
∴BB'=AB+AB'=2+2=4。
故答案为:4。
11. 如图所示,在正方形网格中,图①是由图②经过

平移
变换得到的;图③是由图②经过旋转变换得到的,其旋转中心是点A
(填“A”“B”或“C”)。
答案:
平移 A
12. 如图,△ABC中,AB = BC,将△ABC沿直线BC平移得到△DCE(使点B与点C重合),连接BD,求∠BDE的度数。

解: 由平移可得 $\triangle A B C \cong \triangle D C E$,
$\therefore A B=D C$,
$\because A B=B C, \therefore B C=D C, \therefore \angle D B C=\angle C D B$,
同理可得 $C D=C E, \therefore \angle C D E=\angle E$,
$\therefore 2 \angle C D B+2 \angle C D E=180^{\circ}$,
$\therefore \angle C D B+\angle C D E=90^{\circ}$, 即 $\angle B D E=$

解: 由平移可得 $\triangle A B C \cong \triangle D C E$,
$\therefore A B=D C$,
$\because A B=B C, \therefore B C=D C, \therefore \angle D B C=\angle C D B$,
同理可得 $C D=C E, \therefore \angle C D E=\angle E$,
$\therefore 2 \angle C D B+2 \angle C D E=180^{\circ}$,
$\therefore \angle C D B+\angle C D E=90^{\circ}$, 即 $\angle B D E=$
90°
.
答案:
解: 由平移可得 $\triangle A B C \cong \triangle D C E$,
$\therefore A B=D C$,
$\because A B=B C, \therefore B C=D C, \therefore \angle D B C=\angle C D B$,
同理可得 $C D=C E, \therefore \angle C D E=\angle E$,
$\therefore 2 \angle C D B+2 \angle C D E=180^{\circ}$,
$\therefore \angle C D B+\angle C D E=90^{\circ}$, 即 $\angle B D E=90^{\circ}$.
$\therefore A B=D C$,
$\because A B=B C, \therefore B C=D C, \therefore \angle D B C=\angle C D B$,
同理可得 $C D=C E, \therefore \angle C D E=\angle E$,
$\therefore 2 \angle C D B+2 \angle C D E=180^{\circ}$,
$\therefore \angle C D B+\angle C D E=90^{\circ}$, 即 $\angle B D E=90^{\circ}$.
13. 在平面直角坐标系中,已知点A(2a - b,-8)与点B(-2,a + 3b)关于原点对称,求a、b的值。
答案:
解:
∵点A(2a - b,-8)与点B(-2,a + 3b)关于原点对称,
∴关于原点对称的点的横、纵坐标均互为相反数,
则可得方程组:$\left\{\begin{array}{l}2a - b = 2\\a + 3b = 8\end{array}\right.$
解方程组:
由第一个方程得:$2a - b = 2$,$b = 2a - 2$
将$b = 2a - 2$代入第二个方程$a + 3b = 8$得:
$a + 3(2a - 2) = 8$
$a + 6a - 6 = 8$
$7a = 14$
$a = 2$
将$a = 2$代入$b = 2a - 2$得:$b = 2×2 - 2 = 2$
解得$\left\{\begin{array}{l}a = 2\\b = 2\end{array}\right.$
∵点A(2a - b,-8)与点B(-2,a + 3b)关于原点对称,
∴关于原点对称的点的横、纵坐标均互为相反数,
则可得方程组:$\left\{\begin{array}{l}2a - b = 2\\a + 3b = 8\end{array}\right.$
解方程组:
由第一个方程得:$2a - b = 2$,$b = 2a - 2$
将$b = 2a - 2$代入第二个方程$a + 3b = 8$得:
$a + 3(2a - 2) = 8$
$a + 6a - 6 = 8$
$7a = 14$
$a = 2$
将$a = 2$代入$b = 2a - 2$得:$b = 2×2 - 2 = 2$
解得$\left\{\begin{array}{l}a = 2\\b = 2\end{array}\right.$
14. 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)。
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到$△A_1B_1C_1,$画出$△A_1B_1C_1;$
(2)将$△A_1B_1C_1$绕点$B_1$顺时针旋转90°得到$△A_2B_1C_2,$画出$△A_2B_1C_2;$
(3)线段$B_1C_1$变换到$B_1C_2$的过程中扫过区域的面积为______
(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到$△A_1B_1C_1,$画出$△A_1B_1C_1;$
(2)将$△A_1B_1C_1$绕点$B_1$顺时针旋转90°得到$△A_2B_1C_2,$画出$△A_2B_1C_2;$
(3)线段$B_1C_1$变换到$B_1C_2$的过程中扫过区域的面积为______
4π
。
答案:
【解析】:(1)首先,我们需要确定△ABC各顶点的坐标。假设以网格左下角某个点为原点建立坐标系,通过观察图形可知,点B的坐标为(0,0),点C的坐标为(4,0),点A的坐标为(2,2)(具体坐标需根据网格实际情况确定,此处以常见格点三角形为例)。竖直向上平移6个单位,各点纵坐标加6;再水平向右平移3个单位,各点横坐标加3。则A₁(2+3,2+6)=(5,8),B₁(0+3,0+6)=(3,6),C₁(4+3,0+6)=(7,6),连接A₁、B₁、C₁即可得到△A₁B₁C₁。
(2)将△A₁B₁C₁绕点B₁顺时针旋转90°,根据旋转性质,点B₁位置不变,A₁、C₁绕B₁顺时针旋转90°。点C₁(7,6)相对于B₁(3,6)的坐标差为(4,0),顺时针旋转90°后坐标差变为(0,-4),所以C₂的坐标为(3+0,6-4)=(3,2)。同理可求出A₂的坐标,连接A₂、B₁、C₂得到△A₂B₁C₂。
(3)线段B₁C₁变换到B₁C₂的过程中扫过的区域是以B₁为圆心,B₁C₁为半径,圆心角为90°的扇形。由(1)可知B₁C₁的长度为7-3=4(单位长度),扇形面积公式为$\frac{n\pi r^2}{360}$,其中n=90°,r=4,所以面积为$\frac{90\pi×4^2}{360}=4\pi$。
【答案】:4π
(2)将△A₁B₁C₁绕点B₁顺时针旋转90°,根据旋转性质,点B₁位置不变,A₁、C₁绕B₁顺时针旋转90°。点C₁(7,6)相对于B₁(3,6)的坐标差为(4,0),顺时针旋转90°后坐标差变为(0,-4),所以C₂的坐标为(3+0,6-4)=(3,2)。同理可求出A₂的坐标,连接A₂、B₁、C₂得到△A₂B₁C₂。
(3)线段B₁C₁变换到B₁C₂的过程中扫过的区域是以B₁为圆心,B₁C₁为半径,圆心角为90°的扇形。由(1)可知B₁C₁的长度为7-3=4(单位长度),扇形面积公式为$\frac{n\pi r^2}{360}$,其中n=90°,r=4,所以面积为$\frac{90\pi×4^2}{360}=4\pi$。
【答案】:4π
查看更多完整答案,请扫码查看


