《2025年点对点期末复习及智胜暑假八年级数学北师大版》

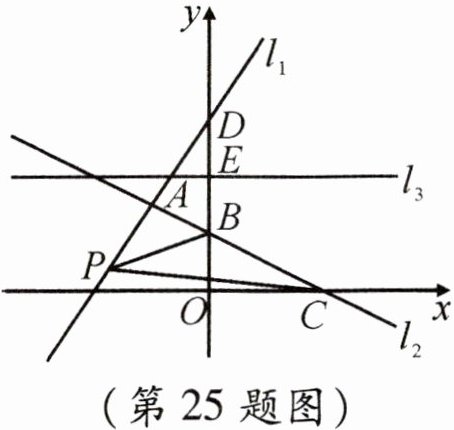
25. 如图,在平面直角坐标系中,直线$l_{1}:y= \frac {3}{2}x+m与直线l_{2}交于点A(-2,3)$,与y轴交于点D,直线$l_{2}$与x轴交于点$C(4,0)$,与y轴交于点B,过BD的中点E作直线$l_{3}⊥y$轴.
(1)求直线$l_{2}$的解析式和m的值;
(2)点P在直线$l_{1}$上,当$S_{\triangle PBC}= 6$时,求点P的坐标;
(3)点P是直线$l_{1}$上一动点,点Q是直线$l_{3}$上一动点,当以点P、Q、B、C为顶点的四边形是平行四边形时,求点Q的坐标.

答案：
解：
(1)$\because A(-2,3)$在直线$l_{1}:y = \frac{3}{2}x + m$上，
$\therefore - 3 + m = 3$，解得$m = 6$。
$\therefore$直线$l_{1}$的解析式为$y = \frac{3}{2}x + 6$。
设直线$l_{2}$的解析式为$y = kx + b$，
$\therefore \begin{cases}4k + b = 0\\- 2k + b = 3\end{cases}$，解得$\begin{cases}k = -\frac{1}{2}\\b = 2\end{cases}$。
$\therefore$直线$l_{2}$的解析式为$y = -\frac{1}{2}x + 2$。
(2)由
(1)可得$B(0,2)$，直线$l_{1}:y = \frac{3}{2}x + 6$。
如图，设直线$PC$与$y$轴交于点$F$。

设$P(t,\frac{3}{2}t + 6)$，直线$PC$的解析式为$y = k_{1}x + b_{1}$，
则$\begin{cases}4k_{1} + b_{1} = 0\\tk_{1} + b_{1} = \frac{3}{2}t + 6\end{cases}$，解得$b_{1} = \frac{6t + 24}{4 - t}$。
$\therefore F(0,\frac{6t + 24}{4 - t})$，$\therefore BF = |\frac{6t + 24}{4 - t} - 2| = |\frac{8t + 16}{4 - t}|$。
$\therefore S_{\triangle PBC} = \frac{1}{2}BF\cdot|x_{C} - x_{P}| = \frac{1}{2}\cdot|\frac{8t + 16}{4 - t}|\cdot|4 - t| = 6$。
化简得$|8t + 16| = 12$，解得$t = -\frac{1}{2}$或$-\frac{7}{2}$。
$\therefore$点$P$的坐标为$(-\frac{1}{2},\frac{21}{4})$或$(-\frac{7}{2},\frac{3}{4})$。
(3)$\because B(0,2)$，$D(0,6)$，$\therefore E(0,4)$。
$\therefore$直线$l_{3}$的解析式为$y = 4$。
设$P(p,\frac{3}{2}p + 6)$，$Q(q,4)$。
①当$PQ$为平行四边形的对角线时，
有$\begin{cases}p + q = 0 + 4\frac{3}{2}p + 6 + 4 = 2 + 0\end{cases}$，解得$\begin{cases}p = -\frac{16}{3}\\q = \frac{28}{3}\end{cases}$，$\therefore Q(\frac{28}{3},4)$。
②当$PB$为平行四边形对角线时，
有$\begin{cases}p + 0 = q + 4\frac{3}{2}p + 6 + 2 = 4 + 0\end{cases}$，解得$\begin{cases}p = -\frac{8}{3}\\q = -\frac{20}{3}\end{cases}$，$\therefore Q(-\frac{20}{3},4)$。
③当$PC$为平行四边形的对角线时，
有$\begin{cases}p + 4 = q + 0\frac{3}{2}p + 6 + 0 = 4 + 2\end{cases}$，解得$\begin{cases}p = 0\\q = 4\end{cases}$，$\therefore Q(4,4)$。
综上所述，点$Q$的坐标为$(\frac{28}{3},4)$或$(-\frac{20}{3},4)$或$(4,4)$。

26. 如图,在$□ ABCD$中,过点C分别作AB、AD的垂线,垂足分别为E、F,$∠ABC$的平分线分别交CE、CF、CD于点M、N、P.
(1)求证:$\triangle CMN$为等腰三角形;
(2)若$AF= \frac {1}{3}FD= \frac {1}{4}CF= 1$,求线段CM的长;
(3)若$AD= CF$,试探究线段CM、FD、AB之间的数量关系,并说明理由.

答案：

(1)证明：$\because$四边形$ABCD$是平行四边形，$\therefore AD// BC$。
$\because CF⊥AD$，$\therefore CF⊥BC$。
$\therefore∠BCF = 90^{\circ}$，$\therefore∠CBN + ∠CNB = 90^{\circ}$。
$\because CE⊥AB$，$\therefore∠BEM = 90^{\circ}$，$\therefore∠EBM + ∠EMB = 90^{\circ}$。
$\because BP$平分$∠ABC$，$\therefore∠ABP = ∠CBP$。
$\therefore∠EMB = ∠CNB$。
$\because∠EMB = ∠CMN$，$\therefore∠CMN = ∠CNM$。
$\therefore\triangle CMN$为等腰三角形。
(2)解：如图1，过点$M$作$MH⊥BC$于点$H$。
$\because AF = \frac{1}{3}DF = \frac{1}{4}CF = 1$，$\therefore FD = 3$，$CF = 4$，$AD = BC = 4$。
$\because∠CFD = 90^{\circ}$，$\therefore CD = AB = \sqrt{FD^{2} + CF^{2}} = 5$。
$\because AB\cdot CE = AD\cdot CF$，$\therefore CE = \frac{16}{5}$。
$\because∠CEB = 90^{\circ}$，$CE = \frac{16}{5}$，$BC = 4$，
$\therefore BE = \sqrt{BC^{2} - CE^{2}} = \frac{12}{5}$。
$\because BP$平分$∠ABC$，$MH⊥BC$，$ME⊥AB$，$\therefore MH = ME$。
设$CM = x$，则$MH = ME = \frac{16}{5} - x$。
$\because∠BEM = ∠BHM$，$∠EBM = ∠HBM$，$BM = BM$，
$\therefore\triangle BEM≌\triangle BHM(AAS)$。
$\therefore BH = BE = \frac{12}{5}$，$\therefore CH = \frac{8}{5}$。
在$Rt\triangle CMH$中，$MH^{2} + CH^{2} = CM^{2}$，
即$(\frac{16}{5} - x)^{2} + (\frac{8}{5})^{2} = x^{2}$，解得$x = 2$。
$\therefore CM = 2$。

(3)解：线段$CM$，$FD$，$AB$之间的数量关系为$CM + FD = AB$。
理由：如图2，在射线$FA$上截取$FQ = CM$，连接$CQ$。
$\because CM = CN$，$FQ = CM$，$\therefore FQ = CN$。
$\because AD = CF$，$AD = BC$，$\therefore BC = CF$。
$\because∠CFQ = ∠BCN = 90^{\circ}$，$\therefore\triangle CFQ≌\triangle BCN(SAS)$。
$\therefore∠Q = ∠CNB$，$∠FCQ = ∠CBN$。
$\because$四边形$ABCD$是平行四边形，
$\therefore AB// CD$，$\therefore∠ABP = ∠CPN$。
$\because BP$平分$∠ABC$，$\therefore∠ABP = ∠CBN$。
$\therefore∠CBN = ∠CPN$，$\therefore∠FCQ = ∠CPN$。
$\therefore∠CPN + ∠PCN = ∠FCQ + ∠PCN$。
$\therefore∠BNC = ∠PCQ$，$\therefore∠PCQ = ∠Q$。
$\therefore DQ = DC = AB$。
$\because FQ + FD = DQ$，$\therefore CM + FD = AB$。