《2025年点对点期末复习及智胜暑假八年级数学北师大版》

26. 阅读材料：如图1,在$△ABC$中,D,E分别是边AB,AC的中点,小明在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,通过延长DE到点F,使$EF= DE$,连接CF,证明$△ADE\cong △CFE$,再证四边形DBCF是平行四边形即得证.
(1)类比迁移：如图2,AD是$△ABC$的中线,BE交AC于点E,交AD于点F,且$AE= EF$,求证：$AC= BF$.小明发现可以类比材料中的思路进行证明.
证明：如图2,延长AD至点M,使$MD= FD$,连接MC,…
请根据小明的思路完成证明过程；
(2)方法运用：如图3,在等边$△ABC$中,D是射线BC上一动点(点D在点C的右侧),连接AD.把线段CD绕点D逆时针旋转$120^{\circ }$得到线段DE.F是线段BE的中点,连接DF,CF.
①请你判断线段DF与AD之间的数量关系,并给出证明；
②若$AB= 8,CF= \frac {1}{2}CD$,请直接写出CF的长.

答案：

(１)证明：如图1，延长AD至点M，使MD = FD．连接MC，
∵AD△ABC的中线，
∴BD = CD，
在△BDF和△CDM中，$\begin{cases}BD = CD\\∠BDF = ∠CDM\\DF = DM\end{cases}$，
∴△BDF ≌ △CDM(SAS)，
∴MC = BF∠M = ∠BFM，
∵AE = EF
∴∠EAF = ∠EFA，
∵∠EFA = ∠BFM，
∴∠M = ∠MAC，
∴AC = MC，
∴AC = BF；

(2)解①线段DF与AD的数量关系为：AD = DF２，
证明如图２延长DF点M，使FM = DF，连接BM、AM，
∵点F为BE的中点，
∴BF = EF．
在△BFM△EFD $\begin{cases}BF = EF\\∠BFM = ∠EFD\\FM = FD\end{cases}$，
∴△BFM ≌ △EFD(SAS)，BM = DE∠MBF = ∠E，BM // DE，
∵线段CD绕点D逆时针旋转120°得到线段DE．
∴CD = DE = BM∠BDE = ∠MBD = 180° - ∠BDE = 60°，
∵△ABC是等边三角形，
∴AB = AC∠ABC = ∠ACB = ∠ABM = ∠ABC + ∠MBD = 120°，
∵∠ACD = ∠ACB = ∠ABM = ∠ACD，△ABM△ACD $\begin{cases}AB = AC\\∠ABM = ∠ACD\\BM = CD\end{cases}$,
∴△ABM ≌ △ACD(SAS),∠BAM = ∠CAD,∠BAC = ∠CAD + ∠BAD = ∠BAM + ∠BAD = 60°,
∴△AMD等边三角形AD = DM = 2DF；
②(i):当CF是△BDE中位线时，CF = $\frac{1}{2}$"CD = $\frac{1}{2}$DEBC = CD = CF = $\frac{１}{2}$CD =４；
(ii):CF不是△BDE的中位线时，

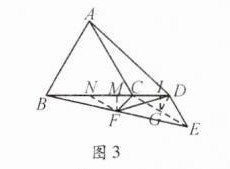
取BC的中点N，连接NF、CENF $\stackrel{//}{=}$" $\frac{1}{２}$"CE，CN = BN = $\frac{1}{2}$"BC = 4，
DGC⊥E于点GFM⊥NC于点MGI⊥CD点I，
∵CD = DE∠CDE = 120°，
"∠CNF = ∠DCE = 3０°，CG = GE = $\frac{１}{2}$"CE，
"NF = CGDG = $\frac{1}{2}$"CD，
"
∵CF = $\frac{１}{2}$"CDCF = DG，
△MNF△ICG $\begin{cases}∠FMN = ∠GIＣ\\∠MNF = ∠ICG\\NF = CG\end{cases}$"，
"△MNF ≌ △ICG(AAS)，NM = CIMF = IG，
Rt△CMF和Rt△DIG $\begin{cases}MF = IG\\CF = DG\end{cases}$"，
"Rt△CMF ≌ Rｔ△DIG(HL)，CM = DI
∴NM + MC = CI + DI，即CN = CD，
"CD =４CF = $\frac{1}{2}$"CD = 2，
综上所述CF的长为4或2。