《2025年实验班提优训练七年级数学上册苏科版》

1. 中考新考法 规律探究 (2023·恩施州中考)观察下列两行数,探究第②行数与第①行数的关系：
-2,4,-8,16,-32,64,…①
0,7,-4,21,-26,71,…②
根据你的发现,完成填空：第①行数的第10个数为1024；取每行数的第2023个数,则这两个数的和为-2²⁰²⁴+2024.

答案： 1024 -2²⁰²⁴+2024 [解析]第①行数的规律为(-2)ⁿ,
∴第①行数的第10个数为(-2)¹⁰=1024;第②行数的规律为(-2)ⁿ+n+1,
∴第①行数的第2023个数为(-2)²⁰²³,第②行数的第2023个数为(-2)²⁰²³+2024,
∴两数之和为-2²⁰²⁴+2024.

2. 图(1)是一个长为2m、宽为2n(m＞n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是多少？

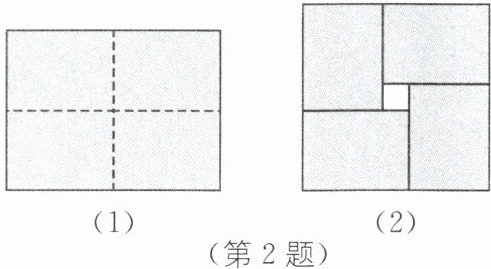
答案：
∵图
(1)是一个长为2m、宽为2n(m＞n)的长方形,
∴图
(2)中大正方形的边长为(m+n),
∴正方形的面积为(m+n)².
∵图
(1)中长方形的面积为2m·2n=4mn,
∴中间空的部分的面积为(m+n)²-4mn.

3. [观察思考]

[规律发现]
(1)第n个图案中“◎”的个数为3n；(请用含n的代数式填空)
(2)第1个图案中“★”的个数可表示为$\frac{1×2}{2},$第2个图案中“★”的个数可表示为$\frac{2×3}{2},$第3个图案中“★”的个数可表示为$\frac{3×4}{2},$…,写出第n个图案中“★”的个数.(请用含n的代数式表示)
$\frac{n(n+1)}{2}$

答案：
(1)3n
(2)$\frac{n(n+1)}{2}$

4. 新情境 购买网球及球拍 为丰富校园体育生活,某校增设网球兴趣小组,需要采购某品牌网球训练拍30支,网球x筒(x＞30),现从甲、乙两家商店了解到该品牌网球拍每支定价均为80元,网球每筒均为20元,并且多买都有一定的优惠.甲商店的优惠条件是：买一支网球拍送一筒网球；乙商店的优惠条件是：网球拍与网球均按9折付款.
(1)选择甲商店购买,所需的费用为20x+1800元；选择乙商店购买,所需的费用为18x+2160元(用含x的代数式表示)；
(2)当购买网球的数量为100筒时,请通过计算说明选择哪家商店所需费用较少.
当x=100时,20x+1800=20×100+1800=3800(元),18x+2160=18×100+2160=3960(元).因为3800＜3960,所以甲商店所需费用较少.

答案：
(1)(20x+1800) (18x+2160)
(2)当x=100时,20x+1800=20×100+1800=3800(元),18x+2160=18×100+2160=3960(元).因为3800＜3960,所以甲商店所需费用较少.