《2025年实验班提优训练七年级数学上册苏科版》

9. 一个立方体的六个面上分别标上一至六点(一个小圆表示一点,每个面上的点数不同),然后将完全一样的四个立方体摆放成如图样式的一个长方体,我们能看到的面上的点数如图所示,则长方体底面上的点数之和是______13。

答案：
(1) - 1 $\frac{1}{2}$ $\frac{1}{3}$
(2)$5a^{2}b - 2(a^{2}b + c) + 3(abc - a^{2}b) - 4abc$
$= 5a^{2}b - 2a^{2}b - 2c + 3abc - 3a^{2}b - 4abc$
$= - 2c - abc$
当$a = - 1$，$b = \frac{1}{2}$，$c = \frac{1}{3}$时，原式$= - 2×\frac{1}{3} - (- 1)×\frac{1}{2}×\frac{1}{3}=-\frac{2}{3}+\frac{1}{6}=-\frac{1}{2}$

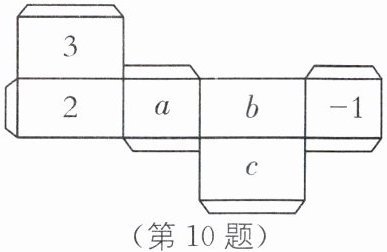
10. 如图是一个长方体形状的包装纸盒的展开图,已知纸盒中相对两个面上的数互为倒数. (1)填空:a=$-\frac{1}{3}$,b=$\frac{1}{2}$,c=$-1$； (2)求代数式 $5a^2b - 2(a^2b + c) + 3(abc - a^2b) - 4abc$ 的值.

(2) 解：原式 $=5a^2b - 2a^2b - 2c + 3abc - 3a^2b - 4abc$
$=(5a^2b - 2a^2b - 3a^2b) + (3abc - 4abc) - 2c$
$=0 - abc - 2c$
$=-abc - 2c$
当 $a = -\frac{1}{3}$，$b = \frac{1}{2}$，$c = -1$ 时，
原式 $=-(-\frac{1}{3})×\frac{1}{2}×(-1) - 2×(-1)$
$=-\frac{1}{6} + 2$
$=\frac{11}{6}$

答案：
(1) $a = -\frac{1}{3}$，$b = \frac{1}{2}$，$c = -1$；
(2) 解：原式 $=5a^2b - 2a^2b - 2c + 3abc - 3a^2b - 4abc$
$=(5a^2b - 2a^2b - 3a^2b) + (3abc - 4abc) - 2c$
$=0 - abc - 2c$
$=-abc - 2c$
当 $a = -\frac{1}{3}$，$b = \frac{1}{2}$，$c = -1$ 时，
原式 $=-(-\frac{1}{3})×\frac{1}{2}×(-1) - 2×(-1)$
$=-\frac{1}{6} + 2$
$=\frac{11}{6}$

11. 中考新考法 课题实践活动 [问题情境] 某综合实践小组进行废物再利用的环保小卫士行动.他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
[操作探究] (1)若准备制作一个无盖的正方体形纸盒,如图(1),图形______经过折叠能围成无盖正方体形纸盒. (2)如图(2)是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是______字. (3)如图(3),有一张边长为20 cm的正方形废弃宣传单,小华准备将其四个角各剪去一个小正方形,折成无盖长方体形纸盒. ①请你在图(3)中画出示意图,用实线表示剪切线,虚线表示折痕. ②若四个角各剪去了一个边长为4 cm的小正方形,则这个纸盒的底面积和容积分别为多少?

答案：

(1)C [解析]无盖，说明展开图是有5个面，由正方体表面展开图“田凹应弃之”可知，选项A不是正方体的表面展开图，而选项B只有4个面，选项D有6个面，故选项C中的图形符合题意。
(2)卫 [解析]由正方体表面展开图的“相间、Z端是对面”可知，“保”与“卫”是对面。
(3)①所画出的图形如图所示。

②当小正方形边长为4cm时，纸盒的底面积为$(20 - 2×4)^{2}=144(cm^{2})$，纸盒的容积为$144×4 = 576(cm^{3})$。故纸盒的底面积为144$cm^{2}$，容积为576$cm^{3}$。
名师点评 本题考查了展开图折叠成几何体的知识，借助几何直观理解问题，运用空间想象认识事物，是直观想象的表现形式，有一定难度，需要学生有一定的想象能力和动手能力。

12. 传统文化 走马灯 (2024·德阳中考)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日.在一次综合实践活动中,一同学用如图所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样,则在A,B,C处依次写上的字可以是(A). A. 吉 如 意 B. 意 吉 如 C. 吉 意 如 D. 意 如 吉

答案： A