第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.(2025·南通期末)下列各式计算结果为负数的是(
A.$3+(-2)$
B.$3-(-2)$
C.$3×(-2)$
D.$(-3)^2$
C
).A.$3+(-2)$
B.$3-(-2)$
C.$3×(-2)$
D.$(-3)^2$
答案:
C
2.(2025·南通启东期末)下列结果最小的是(
A.$-3-\frac{1}{2}$
B.$-3+\frac{1}{2}$
C.$-3×(-\frac{1}{2})$
D.$-3÷(-\frac{1}{2})$
A
).A.$-3-\frac{1}{2}$
B.$-3+\frac{1}{2}$
C.$-3×(-\frac{1}{2})$
D.$-3÷(-\frac{1}{2})$
答案:
A
3.(2024·甘肃白银期末)对于有理数$a,b$,定义一种新运算,规定$a☆b= a^2-|b|$,则$2☆(-3)= $
1
.
答案:
1
4. 教材 P60例4·变式 计算:
(1)$-2^4+(3-7)^2-2$;
(2)$(\frac{1}{2}+\frac{5}{6}-\frac{7}{12})÷(-\frac{1}{6})^2$.
(1)$-2^4+(3-7)^2-2$;
(2)$(\frac{1}{2}+\frac{5}{6}-\frac{7}{12})÷(-\frac{1}{6})^2$.
答案:
(1)原式=-16+(-4)²-2=-16+16-2=0-2=-2.
(2)原式=($\frac{1}{2}+\frac{5}{6}-\frac{7}{12}$)÷$\frac{1}{36}$=($\frac{1}{2}+\frac{5}{6}-\frac{7}{12}$)×36=$\frac{1}{2}$×36+$\frac{5}{6}$×36-$\frac{7}{12}$×36=18+30-21=27.
(1)原式=-16+(-4)²-2=-16+16-2=0-2=-2.
(2)原式=($\frac{1}{2}+\frac{5}{6}-\frac{7}{12}$)÷$\frac{1}{36}$=($\frac{1}{2}+\frac{5}{6}-\frac{7}{12}$)×36=$\frac{1}{2}$×36+$\frac{5}{6}$×36-$\frac{7}{12}$×36=18+30-21=27.
5. 中考新考法 新定义问题 定义:一种对于三位数$\overline{abc}$(其中$a$在百位,$b$在十位,$c$在个位,$a,b,c$不完全相同)的“F运算”:重排$\overline{abc}$的三个数位上的数字,计算所得最大三位数和最小三位数的差(允许百位数字为零),例如$\overline{abc}= 463$时,则$463\xrightarrow{F运算}297$($643 - 346= 297$)$\xrightarrow{F运算}693$($972 - 279= 693$)经过大量运算,我们发现任意一个三位数经过若干次“F运算”都会得到一个固定不变的值;类比联想到:任意一个四位数经过若干次这样的“F运算”也会得到一个定值,这个定值为(
A.4159
B.6419
C.5179
D.6174
D
).A.4159
B.6419
C.5179
D.6174
答案:
D [解析]因为任意一个四位数经过若干次这样的“F 运算”也会得到一个定值,且只要四个数字不完全相同就符合题意,
所以设这个四位数数字为1000,依次进行“F 运算”,得
①1000-0001=0999;②9990-0999=8991;
③9981-1899=8082;④8820-0288=8532;
⑤8532-2358=6174;⑥7641-1467=6174;…
所以这个定值为6174.故选D.
所以设这个四位数数字为1000,依次进行“F 运算”,得
①1000-0001=0999;②9990-0999=8991;
③9981-1899=8082;④8820-0288=8532;
⑤8532-2358=6174;⑥7641-1467=6174;…
所以这个定值为6174.故选D.
6.(2025·扬州邗江区期末)已知$a,b$互为相反数,$c,d$互为倒数,且$|m|= 5$,则$\frac{a+b}{2025}+(-cd)^{2025}+m^2$的值为
24
.
答案:
24 [解析]由题意,可知a+b=0,cd=1,m=±5,
∴$\frac{a+b}{2025}$+(-cd)²⁰²⁵+m²=$\frac{0}{2025}$+(-1)²⁰²⁵+(±5)²=
0-1+25=24.
∴$\frac{a+b}{2025}$+(-cd)²⁰²⁵+m²=$\frac{0}{2025}$+(-1)²⁰²⁵+(±5)²=
0-1+25=24.
7.(1)在玩“24点”游戏时,“3,3,7,7”列式并计算为$7×(3+\frac{3}{7})= 7×3 + 3= 24$是依据运算律:
(2)如图,小明抽到以下4张牌: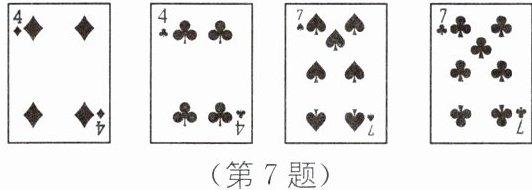 请你帮他写出运算结果为24的一个算式:
请你帮他写出运算结果为24的一个算式:
(3)如果红桃、方片表示正,黑桃、梅花表示负,请你用(2)中的4张牌表示的数写出运算结果为24的一个算式:
乘法分配律
;(2)如图,小明抽到以下4张牌:
 请你帮他写出运算结果为24的一个算式:
请你帮他写出运算结果为24的一个算式:7×(4-$\frac{4}{7}$)
;(3)如果红桃、方片表示正,黑桃、梅花表示负,请你用(2)中的4张牌表示的数写出运算结果为24的一个算式:
-7×($-\frac{4}{7}$-4)
.
答案:
(1)乘法分配律
(2)7×(4-$\frac{4}{7}$)
(3)-7×($-\frac{4}{7}$-4)
(1)乘法分配律
(2)7×(4-$\frac{4}{7}$)
(3)-7×($-\frac{4}{7}$-4)
查看更多完整答案,请扫码查看


