《2025年实验班提优训练七年级数学上册苏科版》

8. (2025·黑龙江绥化期末)最近几年时间,我国的新能源汽车产销量大幅增加,小明家新换了一辆新能源纯电动汽车,他连续 7 天记录了每天行驶的路程(如表),以 50 km 为标准,多于 50 km 的记为“+”,不足 50 km 的记为“-”,刚好 50 km 的记为“0”.

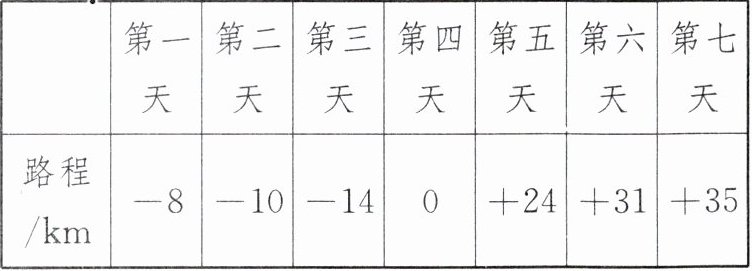
(1)这 7 天里路程最多的一天比最少的一天多走49km.
(2)请求出小明家的新能源汽车这七天一共行驶了多少千米？
50×7+(-8-10-14+0+24+31+35)=350+58=408(千米)，即小明家的新能源汽车这七天一共行驶408千米
(3)已知新能源汽车每行驶 100 km 耗电量为 15 度,每度电为 0.4 元,请计算小明家这 7 天的行驶费用是多少钱？
408÷100×15×0.4=24.48(元)，即小明家这7天的行驶费用是24.48元.

答案：
(1)49
(2)50×7+(-8-10-14+0+24+31+35)=350+58=408(千米)，即小明家的新能源汽车这七天一共行驶408千米
(3)408÷100×15×0.4=24.48(元)，即小明家这7天的行驶费用是24.48元.

9. 已知一列数$2,0,-1,-\frac{1}{2}$.
(1)求最大的数和最小的数的差；
(2)若再添上一个有理数$m$,使得五个有理数的和为 0,求$m$的值.

答案：
(1)2-(-1)=2+1=3.
(2)2+0+(-1)+(-$\frac{1}{2}$)=$\frac{1}{2}$，
∵五个有理数的和为0，
∴$m=-\frac{1}{2}$.

10. (1)有 1,2,3,…,11,12 共 12 个数字,请在每两个数字之间添上“+”或“-”,使它们的和为 0；
(2)若有 1,2,3,…,2023,2024,共 2024 个数字,请在每两个数字之间添上“+”或“-”,使它们的和为 0；
(3)根据(1)(2)的规律,试判断能否在 1,2,3,…,2022,2025,共 2025 个数字的每两个数字之间添上“+”或“-”,使它们的和为 0. 若能,请说明添法；若不能,请说明理由.

答案：
(1)1-2+3-4+5-6-7+8-9+10-11+12=0.(答案不唯一)
(2)1-2+3-4+5-6+...+1011-1012-1013+1014-1015+1016-...-2021+2022-2023+2024=0.(答案不唯一)
(3)不能，因为1到2025的总个数为奇数，每两个数字之间添上“+”或“一”，不能使它们的和为0.