第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
【例1】甲、乙两同学从400米环形跑道上的某一点背向出发,分别以每秒2米和每秒3米的速度跑步.6秒钟后,一只小狗从甲处以每秒6米的速度向乙跑,遇到乙后,又从乙处以每秒6米的速度向甲跑,如此往返直至甲、乙第一次相遇,那么小狗共跑了______米.
解析:设甲、乙同学跑了x秒,则小狗跑了$(x - 6)$秒.
根据题意,得$2x + 3x = 400$,解得$x = 80$.
$80 - 6 = 74$(秒),$74 × 6 = 444$(米).
答案:
解析:设甲、乙同学跑了x秒,则小狗跑了$(x - 6)$秒.
根据题意,得$2x + 3x = 400$,解得$x = 80$.
$80 - 6 = 74$(秒),$74 × 6 = 444$(米).
答案:
444
答案:
解:设甲、乙同学从出发到第一次相遇共跑了$x$秒,则小狗跑了$(x - 6)$秒。
根据题意,得$2x + 3x = 400$,
解得$x = 80$。
小狗跑的时间为:$80 - 6 = 74$(秒),
小狗共跑的路程为:$74×6 = 444$(米)。
答案:444
根据题意,得$2x + 3x = 400$,
解得$x = 80$。
小狗跑的时间为:$80 - 6 = 74$(秒),
小狗共跑的路程为:$74×6 = 444$(米)。
答案:444
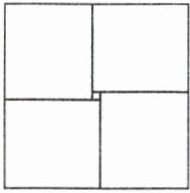
【例2】某同学想用5个边长不等的正方形,拼成如图所示的大正方形.请问该同学的想法能实现吗?如果能实现,试求这5个正方形的边长;如果不能,请说明理由.
解析:此类“是否可行”的问题,通常假设所述的想法能实现,然后列出方程,检验方程的解是否符合题意,如果方程的解符合题意,那么假设成立,即该想法能实现;如果方程没有解或者方程的解不符合题意,那么假设不成立,即该想法不能实现.
答案:不能实现.理由如下:
假设能够实现,不妨设中间小正方形的边长为$x(x > 0)$,左下角的正方形的边长为$y(y > 0)$,则左上角的正方形的边长为$(y - x)$,右上角的正方形的边长为$(y - 2x)$,于是有右下角的正方形的边长为$(y - 3x)或(y + x)$.
所以$y - 3x = y + x$,于是$4x = 0$,得$x = 0$,与$x > 0$矛盾,所以该同学的想法不能实现.
解析:此类“是否可行”的问题,通常假设所述的想法能实现,然后列出方程,检验方程的解是否符合题意,如果方程的解符合题意,那么假设成立,即该想法能实现;如果方程没有解或者方程的解不符合题意,那么假设不成立,即该想法不能实现.

答案:不能实现.理由如下:
假设能够实现,不妨设中间小正方形的边长为$x(x > 0)$,左下角的正方形的边长为$y(y > 0)$,则左上角的正方形的边长为$(y - x)$,右上角的正方形的边长为$(y - 2x)$,于是有右下角的正方形的边长为$(y - 3x)或(y + x)$.
所以$y - 3x = y + x$,于是$4x = 0$,得$x = 0$,与$x > 0$矛盾,所以该同学的想法不能实现.
答案:
【解析】:
本题考查的是利用列方程来解决实际问题。
假设能够实现,设中间小正方形的边长为$x(x > 0)$,左下角的正方形的边长为$y(y > 0)$。
根据正方形的边长关系,则左上角的正方形的边长为$(y - x)$,右上角的正方形的边长为$(y - 2x)$。
所以右下角的正方形的边长为$(y - 3x)$或$(y + x)$。
由于大正方形的边长相等,则有:$y - 3x = y + x$,
移项可得:$4x = 0$,
解得:$x = 0$。
这与$x > 0$矛盾,所以该同学的想法不能实现。
【答案】:
不能实现。理由如下:
假设能够实现,设中间小正方形的边长为$x(x > 0)$,左下角的正方形的边长为$y(y > 0)$,
则左上角的正方形的边长为$(y - x)$,右上角的正方形的边长为$(y - 2x)$,
于是有右下角的正方形的边长为$(y - 3x)$或$(y + x)$。
所以$y - 3x = y + x$,
于是$4x = 0$,
得$x = 0$,
与$x > 0$矛盾,
所以该同学的想法不能实现。
本题考查的是利用列方程来解决实际问题。
假设能够实现,设中间小正方形的边长为$x(x > 0)$,左下角的正方形的边长为$y(y > 0)$。
根据正方形的边长关系,则左上角的正方形的边长为$(y - x)$,右上角的正方形的边长为$(y - 2x)$。
所以右下角的正方形的边长为$(y - 3x)$或$(y + x)$。
由于大正方形的边长相等,则有:$y - 3x = y + x$,
移项可得:$4x = 0$,
解得:$x = 0$。
这与$x > 0$矛盾,所以该同学的想法不能实现。
【答案】:
不能实现。理由如下:
假设能够实现,设中间小正方形的边长为$x(x > 0)$,左下角的正方形的边长为$y(y > 0)$,
则左上角的正方形的边长为$(y - x)$,右上角的正方形的边长为$(y - 2x)$,
于是有右下角的正方形的边长为$(y - 3x)$或$(y + x)$。
所以$y - 3x = y + x$,
于是$4x = 0$,
得$x = 0$,
与$x > 0$矛盾,
所以该同学的想法不能实现。
1. 关于x的方程$ax + b = 0$的解的情况如下:当$a \neq 0$时,方程有唯一解$x = -\frac{b}{a}$;当$a = 0$,$b \neq 0$时,方程无解;当$a = 0$,$b = 0$时,方程有无数解.若关于x的方程$mx + \frac{2}{3} = \frac{n}{3} - x$有无数解,则$m + n$的值为(
A.-1
B.1
C.2
D.以上答案都不对
B
).A.-1
B.1
C.2
D.以上答案都不对
答案:
B [解析]方程整理,得$(m + 1)x + \frac{2}{3} - \frac{n}{3} = 0$,因为关于x的方程有无数解,所以$m + 1 = 0$,$\frac{2}{3} - \frac{n}{3} = 0$,解得$m = -1$,$n = 2$,所以$m + n = -1 + 2 = 1$.故选B.
2. 某列从永川到重庆的火车,包括起始和终点在内共有5个停靠站,小王乘坐这趟列车从永川到重庆,一路上小王在他乘坐的车厢内观测到下列情况:①在起始站(第一站)以后每一站都有车厢内人数(包括小王)的一半人下车;②又有下车人数的一半人上这节车厢;③到第五站(终点站)包括小王在内还有27人.那么起始站上车的人数是______
64
.
答案:
64 [解析]设起始站上车的人数是x人.根据题意得$(\frac{3}{4})^{3}x = 27$,解得$x = 64$.则起始站上车的人数是64.
3. 老师带着两个学生到离学校33千米的博物馆参观.老师骑一辆摩托车,速度为25千米/时,这辆摩托车后座可带乘一名学生,带人后速度为20千米/时,如果学生步行,那么速度为5千米/时.请你设计一种方案,使得师生3人同时出发后用3个小时同时到达博物馆.
答案:
设计方案:学生乙先步行,老师骑摩托车带学生甲行驶一定路程,再让学生甲步行,老师返回接学生乙,然后老师带上学生乙,与学生甲同时到达博物馆即可.关键在确定摩托车中途接乙的返回点.
如图,设两个学生为甲、乙两人.学生乙先步行,老师带学生甲骑摩托车行了x千米,共用了$\frac{x}{20}$小时.他们比乙多行了$\frac{x}{20}(20 - 5) = \frac{3}{4}x$(千米).这时老师让甲步行前进,而自己返回接乙,中途遇到学生乙时,用了$\frac{3}{4}x÷(25 + 5) = \frac{x}{40}$(小时).当乙遇到老师时,已经步行了$(\frac{x}{20} + \frac{x}{40})×5 = \frac{3}{8}x$(千米),离博物馆还有$(33 - \frac{3}{8}x)$千米.若甲、乙两人搭乘摩托车的路程相同,则$x = 33 - \frac{3}{8}x$,解得$x = 24$.这样,在路上学生甲共计用的时间为$\frac{x}{20} + \frac{33 - x}{5} = \frac{24}{20} + \frac{9}{5} = 3$(小时),学生乙共计用的时间为$\frac{x}{20} + \frac{x}{40} + \frac{x}{20} = \frac{24}{8} = 3$(小时).因此,上述方案可使师生3人同时出发后用3小时同时到达博物馆.
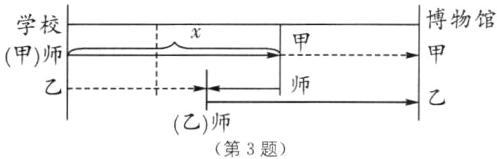
设计方案:学生乙先步行,老师骑摩托车带学生甲行驶一定路程,再让学生甲步行,老师返回接学生乙,然后老师带上学生乙,与学生甲同时到达博物馆即可.关键在确定摩托车中途接乙的返回点.
如图,设两个学生为甲、乙两人.学生乙先步行,老师带学生甲骑摩托车行了x千米,共用了$\frac{x}{20}$小时.他们比乙多行了$\frac{x}{20}(20 - 5) = \frac{3}{4}x$(千米).这时老师让甲步行前进,而自己返回接乙,中途遇到学生乙时,用了$\frac{3}{4}x÷(25 + 5) = \frac{x}{40}$(小时).当乙遇到老师时,已经步行了$(\frac{x}{20} + \frac{x}{40})×5 = \frac{3}{8}x$(千米),离博物馆还有$(33 - \frac{3}{8}x)$千米.若甲、乙两人搭乘摩托车的路程相同,则$x = 33 - \frac{3}{8}x$,解得$x = 24$.这样,在路上学生甲共计用的时间为$\frac{x}{20} + \frac{33 - x}{5} = \frac{24}{20} + \frac{9}{5} = 3$(小时),学生乙共计用的时间为$\frac{x}{20} + \frac{x}{40} + \frac{x}{20} = \frac{24}{8} = 3$(小时).因此,上述方案可使师生3人同时出发后用3小时同时到达博物馆.

查看更多完整答案,请扫码查看


