《2025年实验班提优训练七年级数学上册苏科版》

1. (2025·湖北武汉期末)下列说法正确的是(D).
A.一个角的补角一定大于这个角
B.任何一个角都有余角
C.若∠1+∠2+∠3= 180°,则∠1,∠2,∠3互补
D.若一个角有余角,则这个角的补角与这个角的余角的差为 90°

答案： D [解析] A. 一个角的补角不一定大于这个角,选项说法错误,不符合题意;
B. 任何一个锐角都有余角,选项说法错误,不符合题意;
C. 若两角的和等于180度,则这两角互补,选项说法错误,不符合题意;
D. 若一个角有余角,则这个角的补角与这个角的余角的差为90°,选项说法正确,符合题意.
故选 D.

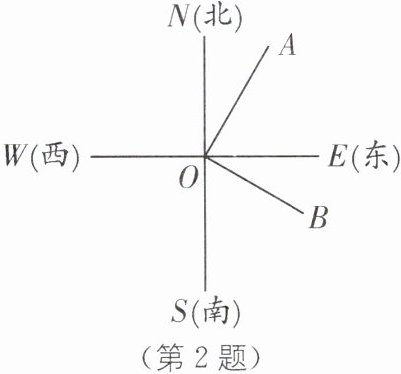
2. (2025·浙江余姚期末)如图,货轮 O 在航行的过程中发现灯塔 A 在它的北偏东 30°的方向上,海岛 B 在它南偏东 60°方向上. 则下列结论：①∠NOA= 30°；②图中∠NOB 的补角有两个,分别是∠BOS 和∠EOA；③图中有 4 对互余的角；④货轮 O 在海岛 B 的北偏西 60°的方向上. 其中正确结论的个数有(D).


A.1 个
B.2 个
C.3 个
D.4 个

答案： D [解析] 由方位角意义可知∠NOA=30°,因此①正确;根据题意可求出∠NOB=120°,∠SOB=60°,∠EOA=60°,因此②正确;图中互余的角有∠NOA 和∠AOE,∠NOA 和∠BOS,∠BOE 和∠AOE,∠BOE 和∠BOS,因此③正确;根据方位角,海岛 B 在轮船 O 南偏东60°方向,即∠BOS=60°,也就是∠BOE=30°,反之货轮 O 在海岛 B 的北偏西60°的方向上,因此④正确.综上所述,正确的个数有4个.故选 D.

3. (2025·杭州西湖区期末)已知∠1 与∠2 互为余角,∠1 与∠3 互为补角,有以下三个结论：①∠3= 90°+∠2；②∠3= 2∠1+∠2；③∠3-∠1＞∠2. 其中正确的结论是(A).
A.①③
B.①
C.③
D.①②③

答案： A [解析] 由题意,得∠1+∠2=90°,∠1+∠3=180°,得∠3=180°-∠1=2∠1+2∠2-∠1=∠1+2∠2,
∴∠3-∠1＞∠2,
∴②错误,③正确.
∵∠1+∠2=90°,∠1+∠3=180°,
∴∠3=∠2+90°,
∴①正确.故选 A.

4. (2025·安徽合肥庐江期末)如果∠α和∠β互补,且∠α＜∠β,则下列表示∠α的余角的式子中：①90°-∠α；②∠β-90°；③$\frac{1}{2}$(∠α+∠β)；④$\frac{1}{2}$(∠β-∠α),其中正确的有(C).
A.1 个
B.2 个
C.3 个
D.4 个

答案： C [解析]
∵∠α的余角为90°-∠α,故①正确;∠α的余角为90°-∠α=90°-(180°-∠β)=∠β-90°,故②正确;
∵∠α和∠β互补,
∴∠α+∠β=180°,
∴∠α=180°-∠β,
∴$\frac{1}{2}$∠α+$\frac{1}{2}$∠β=90°.∠α的余角为90°-∠α=$\frac{1}{2}$∠α+$\frac{1}{2}$∠β-∠α=$\frac{1}{2}$∠β-$\frac{1}{2}$∠α,故④正确;
∵$\frac{1}{2}$(∠α+∠β)=90°,
∴∠α不一定是锐角,故③不正确.因此正确的有①②④,共3个.故选 C.

5. 方程思想 (2025·江西赣州大余期末)有一个角的余角比这个角的补角的一半还少 8°,那么这个角的余角是多少度？

答案： 设这个角为x,则这个角的余角为90°-x,这个角的补角为180°-x,则90°-x=$\frac{1}{2}$(180°-x)-8°,解得x=16°.故这个角的余角为90°-16°=74°.

6. (2025·福建福州平潭期末)若一个锐角的度数为 x,且这个锐角比它的余角小 30°.
(1)这个锐角的余角为90°-x(或x+30°)；
(2)求这个锐角的度数.
根据题意,得x=90°-x-30°,解得x=30°.故这个锐角的度数为30°.

答案：
(1)90°-x(或x+30°)
(2)根据题意,得x=90°-x-30°,解得x=30°.故这个锐角的度数为30°.

7. (2025·河南信阳期末)如图,两个直角三角形的直角顶点重合.
(1)若∠BOD= 40°,求∠AOC 的度数.
解：∵∠AOC + ∠COB = 90°,∠COB + ∠BOD= 90°,…①
∴∠AOC=∠BOD,…②
∵∠BOD= 40°,
∴∠AOC=40°.
把上面过程补充完整,并回答：在上面①到②的推导过程中,理论依据是同角的余角相等；
(2)写出图中互为补角的角∠AOB 与∠COD,∠AOD 与∠BOC；
(3)若 OB 平分∠COD,求∠AOD 的度数.
∵∠COD=90°,且 OB 平分∠COD,∴∠BOC=∠BOD=$\frac{1}{2}$∠COD=45°,（角平分线定义）∴∠AOD=∠AOB+∠BOD=90°+45°=135°.

答案：
(1)∠BOD 40 同角的余角相等
(2)∠AOB 与∠COD,∠AOD 与∠BOC [解析]
∵∠AOB=90°,∠COD=90°,
∴∠AOB+∠COD=180°,即∠AOB 与∠COD 互为补角,
∴∠AOC+∠COD+∠BOC=180°,即∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互为补角.
(3)
∵∠COD=90°,且 OB 平分∠COD,
∴∠BOC=∠BOD=$\frac{1}{2}$∠COD=45°,
角平分线定义
∴∠AOD=∠AOB+∠BOD=90°+45°=135°.