第121页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.(2024·江西吉安吉州区期中)填空:已知∠AOB= 90°,∠COD= 90°,OE平分∠BOD,∠AOC= 30°.
(1)如图,OC在∠AOB内部时,求∠COE的度数.
解:∵∠AOB= 90°,∴∠BOC+∠AOC= 90°.
∵∠COD= 90°,∴∠BOC+∠BOD= 90°,
∴∠AOC= ∠BOD(______)(填写推理依据).
∵∠AOC= 30°,∴∠BOD= 30°.
∵OE平分∠BOD,
∴∠DOE= ______= ______°(______)(填写推理依据),
∴∠COE= ∠COD-∠DOE= ______°.
(2)若OC在∠AOB外部,∠COE的度数为______.
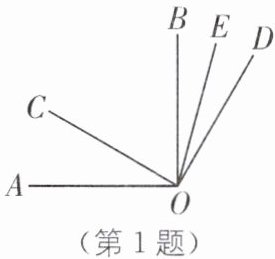

(1)如图,OC在∠AOB内部时,求∠COE的度数.
解:∵∠AOB= 90°,∴∠BOC+∠AOC= 90°.
∵∠COD= 90°,∴∠BOC+∠BOD= 90°,
∴∠AOC= ∠BOD(______)(填写推理依据).
∵∠AOC= 30°,∴∠BOD= 30°.
∵OE平分∠BOD,
∴∠DOE= ______= ______°(______)(填写推理依据),
∴∠COE= ∠COD-∠DOE= ______°.
(2)若OC在∠AOB外部,∠COE的度数为______.


答案:
同角的余角相等 ∠BOE 15 角平分线的定义 75
(2)165°或105° [解析]分情况讨论:
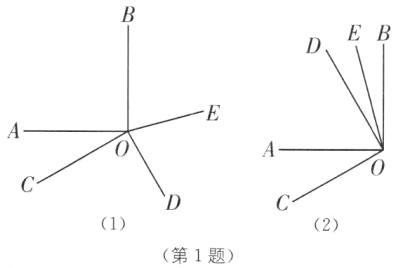
①如图
(1),当 OD 在∠AOB 外部时,
∵∠AOB=90°,∠COD=90°,∠AOC=30°,
∴∠BOD=360°-90°-90°-30°=150°.
∵OE 平分∠BOD,
∴∠DOE=$\frac{1}{2}$∠BOD=75°,
∴∠COE=∠COD + ∠DOE=90°+75°=165°.
②如图
(2),当 OD 在∠AOB 内部时,
∵∠AOB=90°,∠COD=90°,∠AOC=30°,
∴∠BOD=30°.
∵OE 平分∠BOD,
∴∠DOE=15°.
∴∠COE=∠COD + ∠DOE=90°+15°=105°.
关键提醒 本题考查了余角和周角、角平分线的定义,熟练掌握同角的余角相等是解题的关键.
同角的余角相等 ∠BOE 15 角平分线的定义 75
(2)165°或105° [解析]分情况讨论:
①如图
(1),当 OD 在∠AOB 外部时,
∵∠AOB=90°,∠COD=90°,∠AOC=30°,
∴∠BOD=360°-90°-90°-30°=150°.
∵OE 平分∠BOD,
∴∠DOE=$\frac{1}{2}$∠BOD=75°,
∴∠COE=∠COD + ∠DOE=90°+75°=165°.
②如图
(2),当 OD 在∠AOB 内部时,
∵∠AOB=90°,∠COD=90°,∠AOC=30°,
∴∠BOD=30°.
∵OE 平分∠BOD,
∴∠DOE=15°.
∴∠COE=∠COD + ∠DOE=90°+15°=105°.

关键提醒 本题考查了余角和周角、角平分线的定义,熟练掌握同角的余角相等是解题的关键.
变式1.1 (2025·北京怀柔区期末)如图是某航海区域的情况,在灯塔O附近有A,B,C,D,E,F六座海轮,其中F到灯塔的距离为10 km,海轮F在灯塔和海轮D的中点处.且∠AOD= 42°30′,∠DOE= ∠AOC= 78.5°.则下列说法正确的是(
①若海轮F的速度为30 km/h,则海轮F抵达灯塔需要20 min;②∠EOC= 43°;③∠BOE= 59°;④C在灯塔的北偏东11°30′的方向上.
A.①④
B.①②
C.①③④
D.①②③④
C
).①若海轮F的速度为30 km/h,则海轮F抵达灯塔需要20 min;②∠EOC= 43°;③∠BOE= 59°;④C在灯塔的北偏东11°30′的方向上.
A.①④
B.①②
C.①③④
D.①②③④
答案:
C [解析]①若海轮 F 的速度为 30 km/h,则海轮 F 抵达灯塔需要$\frac{10}{30}$h = 20 min,故①正确;②
∵∠DOE=∠AOC,
∴∠DOE - ∠COD=∠AOC - ∠COD,
∴∠EOC=∠AOD=42°30',故②错误;③∠BOE=180° - ∠AOD - ∠DOE=180° - 42°30' - 78.5°=59°,故③正确;④
∵90° - ∠AOC=11°30',
∴C 在灯塔的北偏东 11°30'的方向上,故④正确.故选 C.
∵∠DOE=∠AOC,
∴∠DOE - ∠COD=∠AOC - ∠COD,
∴∠EOC=∠AOD=42°30',故②错误;③∠BOE=180° - ∠AOD - ∠DOE=180° - 42°30' - 78.5°=59°,故③正确;④
∵90° - ∠AOC=11°30',
∴C 在灯塔的北偏东 11°30'的方向上,故④正确.故选 C.
变式1.2 (2025·陕西西安高陵区期末)[问题背景]已知OB是∠AOC内部的一条射线,OM是∠AOB内部的一条射线,ON是∠BOC内部的一条射线.
[初步探究](1)如图(1),已知∠AOB= 30°,OM是∠AOB的角平分线.
①则∠AOM= ______
②若∠MON= 70°,ON是∠BOC的角平分线,求∠BOC的度数.
[拓展提升](2)如图(2),若∠AOC= 140°,∠AOB= 4∠AOM= 4∠CON,且$∠BON= \frac{2}{3}∠BOM,$求∠MON的度数.

[初步探究](1)如图(1),已知∠AOB= 30°,OM是∠AOB的角平分线.
①则∠AOM= ______
15°
;②若∠MON= 70°,ON是∠BOC的角平分线,求∠BOC的度数.
∵∠AOB=30°,OM 是∠AOB 的平分线,∴∠BOM=∠AOM=15°.∵∠MON=70°,∴∠BON=∠MON - ∠BOM=55°.∵ON 平分∠BOC,∴∠BOC=2∠BON=110°.
[拓展提升](2)如图(2),若∠AOC= 140°,∠AOB= 4∠AOM= 4∠CON,且$∠BON= \frac{2}{3}∠BOM,$求∠MON的度数.
设∠AOM=∠CON=α,则∠AOB=4α.∵∠BOM=∠AOB - ∠AOM,∴∠BOM=4α - α=3α.∵∠BON=$\frac{2}{3}$∠BOM,∴∠BON=2α.∵∠AOC=∠AOB + ∠BON + ∠CON=140°,∴4α + 2α + α=140°,∴α=20°.∵∠MON=∠BOM + ∠BON,∴∠MON=3α + 2α=100°.

答案:
(1)①15° [解析]
∵∠AOB=30°,OM 是∠AOB 的角平分线,
∴∠AOM=$\frac{1}{2}$∠AOB=15°.
②
∵∠AOB=30°,OM 是∠AOB 的平分线,
∴∠BOM=∠AOM=15°.
∵∠MON=70°,
∴∠BON=∠MON - ∠BOM=55°.
∵ON 平分∠BOC,
∴∠BOC=2∠BON=110°.
(2)设∠AOM=∠CON=α,则∠AOB=4α.
∵∠BOM=∠AOB - ∠AOM,
∴∠BOM=4α - α=3α.
∵∠BON=$\frac{2}{3}$∠BOM,
∴∠BON=2α.
∵∠AOC=∠AOB + ∠BON + ∠CON=140°,
∴4α + 2α + α=140°,
∴α=20°.
∵∠MON=∠BOM + ∠BON,
∴∠MON=3α + 2α=100°.
(1)①15° [解析]
∵∠AOB=30°,OM 是∠AOB 的角平分线,
∴∠AOM=$\frac{1}{2}$∠AOB=15°.
②
∵∠AOB=30°,OM 是∠AOB 的平分线,
∴∠BOM=∠AOM=15°.
∵∠MON=70°,
∴∠BON=∠MON - ∠BOM=55°.
∵ON 平分∠BOC,
∴∠BOC=2∠BON=110°.
(2)设∠AOM=∠CON=α,则∠AOB=4α.
∵∠BOM=∠AOB - ∠AOM,
∴∠BOM=4α - α=3α.
∵∠BON=$\frac{2}{3}$∠BOM,
∴∠BON=2α.
∵∠AOC=∠AOB + ∠BON + ∠CON=140°,
∴4α + 2α + α=140°,
∴α=20°.
∵∠MON=∠BOM + ∠BON,
∴∠MON=3α + 2α=100°.
2.(2025·河南漯河舞阳县期末)如图,OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC的平分线,OP是∠NOA平分线,OQ是∠MOA的平分线,则∠POQ:∠BOC= (

A.1:2
B.1:3
C.2:5
D.1:4
D
).
A.1:2
B.1:3
C.2:5
D.1:4
答案:
D [解析]
∵OM 是∠AOB 的平分线,OQ 是∠MOA 平分线,
∴∠AOQ=$\frac{1}{2}$∠AOM=$\frac{1}{4}$∠AOB.
∵ON 是∠AOC 的平分线,OP 是∠NOA 的平分线,
∴∠AOP=$\frac{1}{2}$∠AON=$\frac{1}{4}$∠AOC=$\frac{1}{4}$(∠AOB + ∠BOC),
∴∠POQ=∠AOP - ∠AOQ=$\frac{1}{4}$(∠AOB + ∠BOC) - $\frac{1}{4}$∠AOB=$\frac{1}{4}$∠BOC,
∴∠POQ:∠BOC=1:4.
故选 D.
∵OM 是∠AOB 的平分线,OQ 是∠MOA 平分线,
∴∠AOQ=$\frac{1}{2}$∠AOM=$\frac{1}{4}$∠AOB.
∵ON 是∠AOC 的平分线,OP 是∠NOA 的平分线,
∴∠AOP=$\frac{1}{2}$∠AON=$\frac{1}{4}$∠AOC=$\frac{1}{4}$(∠AOB + ∠BOC),
∴∠POQ=∠AOP - ∠AOQ=$\frac{1}{4}$(∠AOB + ∠BOC) - $\frac{1}{4}$∠AOB=$\frac{1}{4}$∠BOC,
∴∠POQ:∠BOC=1:4.
故选 D.
查看更多完整答案,请扫码查看


