第113页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1.(2025·广西梧州苍梧期末)如图,下列表示角的说法,错误的是(
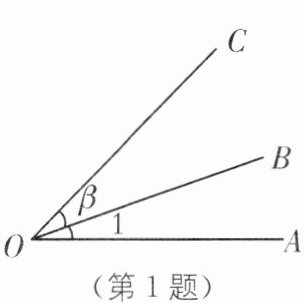
A.∠AOC也可用∠O表示
B.∠1与∠AOB表示同一个角
C.∠β表示的是∠BOC
D.∠AOB和∠BOC都不能用∠O表示
A
).
A.∠AOC也可用∠O表示
B.∠1与∠AOB表示同一个角
C.∠β表示的是∠BOC
D.∠AOB和∠BOC都不能用∠O表示
答案:
A
2.(2024·南京秦淮区期末)用一副直角三角板,不能画出的角是(
A.15°
B.75°
C.145°
D.165°
C
).A.15°
B.75°
C.145°
D.165°
答案:
C [解析]一副直角三角板的6个角的度数分别为30°,60°,90°,45°,45°,90°.A.
∵45°−30°=15°,
∴用三角板能够画出15°的角,故此选项不符合题意;B.
∵30°+45°=75°,
∴用三角板能够画出75°的角,故此选项不符合题意;C.
∵90°+55°=45°+30°+70°=60°+45°+40°=145°,
∴用三角板不能画出145°的角,故此选项符合题意;D.
∵90°+45°+30°=165°,
∴用三角板能够画出165°的角,故此选项不符合题意.故选C;
∵45°−30°=15°,
∴用三角板能够画出15°的角,故此选项不符合题意;B.
∵30°+45°=75°,
∴用三角板能够画出75°的角,故此选项不符合题意;C.
∵90°+55°=45°+30°+70°=60°+45°+40°=145°,
∴用三角板不能画出145°的角,故此选项符合题意;D.
∵90°+45°+30°=165°,
∴用三角板能够画出165°的角,故此选项不符合题意.故选C;
3.如图,∠1,∠2表示的角可分别用大写字母表示为
∠ABC
,∠BCN
;∠A也可表示为∠BAC
,还可以表示为∠MAN(或∠MAC或∠BAN)
.
答案:
∠ABC ∠BCN ∠BAC ∠MAN(或∠MAC或∠BAN)
4.比较大小:32°15′
>
32.15°(填“>”或“<”).
答案:
>
5.教材P164练习T3·变式 计算:(结果用度、分、秒表示)
(1)$23^\circ30'45'' + 40^\circ45'20''$;
(2)$180^\circ - 70^\circ40'$.
(1)$23^\circ30'45'' + 40^\circ45'20''$;
(2)$180^\circ - 70^\circ40'$.
答案:
(1)64°16'5''
(2)109°20'
(1)64°16'5''
(2)109°20'
6.(2024·北京顺义区期末)下列图形中,能用∠1,∠A,∠BAD三种方法表示同一个角的图形是(
A
).
答案:
A [解析]A.以A为顶点的角有一个,可用∠1,∠A,∠BAD三种方法表示同一个角,符合题意;B.不能用∠1,∠A,∠BAD三种方法表示同一个角,不符合题意;C.∠1与∠A,∠BAD不是同一个顶点,∠1,∠A,∠BAD三种方法表示不是同一个角,不符合题意;D.不能用∠1,∠A,∠BAD三种方法表示同一个角,不符合题意.故选A
7.(2025·宿迁宿城区期末)如图是一副特制的三角板,仅用这副特制的三角板不能画出的角度是(

A.84°
B.68°
C.48°
D.24°
B
).
A.84°
B.68°
C.48°
D.24°
答案:
B
8.(2024·南京外国语学校期末)A,B两个海上观测站的位置如图所示,A在灯塔O北偏东40°方向上,∠AOB= 110°,则B在灯塔O的
南偏东30°
方向.
答案:
南偏东30° [解析]由题意,得180°−40°−110°=30°,
∴B在灯塔O的南偏东30°方向
∴B在灯塔O的南偏东30°方向
9.(2025·陕西西安临潼期末)如图所示,在已知锐角∠AOB内部,画1条射线,图中共有3个角;画2条射线,图中共有6个角;画3条射线,图中共有10个角;按此规律,…,画n条射线,共有
$\frac{(n+1)(n+2)}{2}$
个角.
答案:
$\frac{(n+1)(n+2)}{2}$ [解析]根据题意,分析出射线的条数与角的数量关系如下:画1条射线,图中共有3个角=$\frac{(1+1)(1+2)}{2}$;画2条射线,图中共有6个角=$\frac{(2+1)(2+2)}{2}$;画3条射线,图中共有10个角=$\frac{(3+1)(3+2)}{2}$;
∴画n条射线,图中共有$\frac{(n+1)(n+2)}{2}$个角.
∴画n条射线,图中共有$\frac{(n+1)(n+2)}{2}$个角.
查看更多完整答案,请扫码查看


