第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 中考新考法 证明代数结论 (2025·浙江绍兴越城区期末)
日常生活中,我们常常将“八点五十五分”说成“九点差五分”,有时这样表达更清楚. 这就启发我们设计了一种新的加减记数法. 例如:9 可写成$1\overline{1}$,$1\overline{1}= 10-1$;198 可写成$20\overline{2}$,$20\overline{2}= 200-2$;7683 可写成$\overline{1232}3$,$\overline{1232}3= 10000-2320+3$. 总之,数字上画一杠表示减去“它”,按这个方法计算:$5\overline{23}\overline{1}-3\overline{24}1= $
日常生活中,我们常常将“八点五十五分”说成“九点差五分”,有时这样表达更清楚. 这就启发我们设计了一种新的加减记数法. 例如:9 可写成$1\overline{1}$,$1\overline{1}= 10-1$;198 可写成$20\overline{2}$,$20\overline{2}= 200-2$;7683 可写成$\overline{1232}3$,$\overline{1232}3= 10000-2320+3$. 总之,数字上画一杠表示减去“它”,按这个方法计算:$5\overline{23}\overline{1}-3\overline{24}1= $
2068
.
答案:
2 068 [解析]523ˉ¹-324ˉ¹=(5 000-200)+(30-1)-[3 000-240+1]=4 800+29-2 761=4 829-2 761=2 068. 归纳总结 本题主要考查有理数的混合运算,解答的关键是理解清楚所给的记数方式.
2. 计算:
(1)$-5-(-3)+(-4)-[-(-2)]$;
(2)$\frac{2}{3}+(\frac{5}{6}+2.8+\frac{1}{3})-(2\frac{4}{5}+\frac{5}{6})$;
(3)$-(-\frac{3}{2})+(-\frac{5}{6})+[\frac{11}{4}-(-\frac{3}{8})-(+\frac{14}{3})]$.
(1)$-5-(-3)+(-4)-[-(-2)]$;
(2)$\frac{2}{3}+(\frac{5}{6}+2.8+\frac{1}{3})-(2\frac{4}{5}+\frac{5}{6})$;
(3)$-(-\frac{3}{2})+(-\frac{5}{6})+[\frac{11}{4}-(-\frac{3}{8})-(+\frac{14}{3})]$.
答案:
(1)原式=-5+3-4-2=-8.
(2)原式=$\frac{2}{3}+\frac{5}{6}+2.8+\frac{1}{3}-2\frac{4}{5}-\frac{5}{6}=1$.
(3)原式=$\frac{3}{2}-\frac{5}{6}+\frac{11}{4}+\frac{3}{8}-\frac{14}{3}$
=$\frac{36}{24}-\frac{20}{24}+\frac{66}{24}+\frac{9}{24}-\frac{112}{24}$
=$\frac{36-20+66+9-112}{24}=-\frac{7}{8}$.
(1)原式=-5+3-4-2=-8.
(2)原式=$\frac{2}{3}+\frac{5}{6}+2.8+\frac{1}{3}-2\frac{4}{5}-\frac{5}{6}=1$.
(3)原式=$\frac{3}{2}-\frac{5}{6}+\frac{11}{4}+\frac{3}{8}-\frac{14}{3}$
=$\frac{36}{24}-\frac{20}{24}+\frac{66}{24}+\frac{9}{24}-\frac{112}{24}$
=$\frac{36-20+66+9-112}{24}=-\frac{7}{8}$.
3. 传统文化 “铺地锦” 我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法,称为“铺地锦”. 例如,如图(1)所示,计算$31×47$,首先把乘数 31 和 47 分别写在方格的上面和右面,然后以 31 的每位数字分别乘 47 的每位数字,将结果计入对应的格子中(如$3×4= 12$的 12 写在 3 下面的方格里,十位 1 写在斜线的上面,个位 2 写在斜线的下面),再把同一斜线上的数相加,结果写在斜线末端,最后把得数依次写下来是 1457,即$31×47= 1457$. 如图(2),用“铺地锦”的方法表示两个两位数相乘,则a的值是(
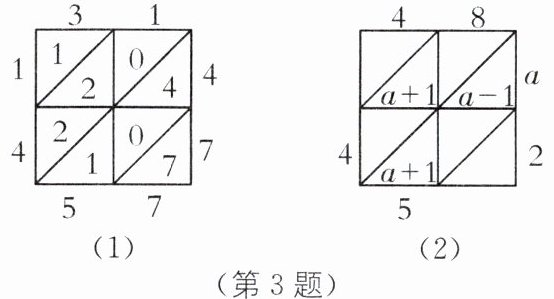
A.2
B.3
C.5
D.7
D
).
A.2
B.3
C.5
D.7
答案:
D
4. 计算:
(1)$[2\frac{1}{2}-(-1\frac{1}{2})]÷(-\frac{1}{4})×(-\frac{1}{8})$;
(2)$18÷\left\{1\frac{5}{12}-\left[2\frac{4}{5}÷(-3\frac{9}{25})-0.75\right]\right\}$.
(1)$[2\frac{1}{2}-(-1\frac{1}{2})]÷(-\frac{1}{4})×(-\frac{1}{8})$;
(2)$18÷\left\{1\frac{5}{12}-\left[2\frac{4}{5}÷(-3\frac{9}{25})-0.75\right]\right\}$.
答案:
(1)原式=4×(-4)×$(-\frac{1}{8})=2$.
(2)原式=18÷$(1\frac{5}{12}+2\frac{4}{5}÷3\frac{9}{25}+\frac{3}{4})$
=18÷$(1\frac{5}{12}+\frac{5}{6}+\frac{3}{4})=18÷3=6$.
(1)原式=4×(-4)×$(-\frac{1}{8})=2$.
(2)原式=18÷$(1\frac{5}{12}+2\frac{4}{5}÷3\frac{9}{25}+\frac{3}{4})$
=18÷$(1\frac{5}{12}+\frac{5}{6}+\frac{3}{4})=18÷3=6$.
查看更多完整答案,请扫码查看


