第110页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. (2025·山东济宁汶上期末)如图,点 C 为线段 AB 的中点,点 D 为线段 CB 上任意一点,则下列表示线段关系的式子中不正确的是(
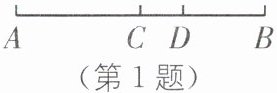
A.$AB= 2AC$
B.$AC+CD+DB= AB$
C.$CD= AD-\frac{1}{2}AB$
D.$AD= \frac{1}{2}(CD+AB)$
]
D
).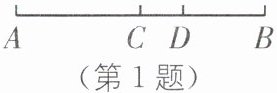
A.$AB= 2AC$
B.$AC+CD+DB= AB$
C.$CD= AD-\frac{1}{2}AB$
D.$AD= \frac{1}{2}(CD+AB)$
]
答案:
D
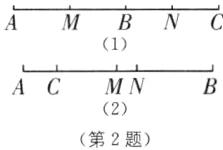
2. 分类讨论思想 两根木条,一根长 10 cm,另一根长 12 cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( ).
A.1 cm
B.11 cm
C.1 cm 或 11 cm
D.2 cm 或 11 cm
A.1 cm
B.11 cm
C.1 cm 或 11 cm
D.2 cm 或 11 cm
答案:
C [解析]如图,设较长的木条为AB=12cm,较短的木条为BC=10cm.
∵M,N分别为AB,BC的中点,
∴BM=6cm,BN=5cm.
①如图
(1),当线段BC不在线段AB上时,MN=BM+BN=6+5=11(cm);
②如图
(2),当线段BC在线段AB上时,MN=BM - BN=6−5=1(cm).
综上所述,两根木条的中点间的距离是1cm或11cm.故选C.
C [解析]如图,设较长的木条为AB=12cm,较短的木条为BC=10cm.
∵M,N分别为AB,BC的中点,
∴BM=6cm,BN=5cm.
①如图
(1),当线段BC不在线段AB上时,MN=BM+BN=6+5=11(cm);
②如图
(2),当线段BC在线段AB上时,MN=BM - BN=6−5=1(cm).
综上所述,两根木条的中点间的距离是1cm或11cm.故选C.

3. (2025·南通海安北城中学期末)如图,点 C,D 在线段 AB 上,点 C 为 AB 中点,若 $AC= 5\ cm$,$BD= 2\ cm$,则 $CD=$
3
cm.
答案:
3
4. 已知线段 $AB= 2\ cm$,延长 AB 到点 C,使 $BC= 4\ cm$,若点 D 为 AB 的中点,则线段 $DC= $______.
答案:
5cm [解析]根据题意,画出图形如图所示:

∵AB=2cm,BC=4cm,
∴DC=DB+BC=$\frac{1}{2}$AB+BC=$\frac{1}{2}$×2+4=5(cm).
归纳总结 本题考查的是两点间距离,熟知各线段之间的和、差及倍数关系是解题的关键.
5cm [解析]根据题意,画出图形如图所示:

∵AB=2cm,BC=4cm,
∴DC=DB+BC=$\frac{1}{2}$AB+BC=$\frac{1}{2}$×2+4=5(cm).
归纳总结 本题考查的是两点间距离,熟知各线段之间的和、差及倍数关系是解题的关键.
5. 教材 P161 习题 T6·变式 如图,点 C 为线段 AD 上一点,点 B 为 CD 的中点,$AD= 20\ cm$,$AC= 12\ cm$.
(1)写出图中所有线段;
(2)求 AB 的长.
]

(1)写出图中所有线段;
(2)求 AB 的长.
]

答案:
(1)图中线段有AC,AB,AD,CB,CD,BD.
(2)
∵AD=20cm,AC=12cm,
∴CD=AD−AC=20−12=8(cm).
∵点B为CD的中点,CB=$\frac{1}{2}$CD=4cm,
∴AB=AC+CB=12+4=16(cm).
(1)图中线段有AC,AB,AD,CB,CD,BD.
(2)
∵AD=20cm,AC=12cm,
∴CD=AD−AC=20−12=8(cm).
∵点B为CD的中点,CB=$\frac{1}{2}$CD=4cm,
∴AB=AC+CB=12+4=16(cm).
6. (2025·浙江杭州滨江区期末)已知点 A,B,C 是直线 l 上互不重合的三个点,设 $AB= 3a$,$AC= na+2$,$BC= a+6$,其中 n 是自然数,a 是正数,(
A.若 $n= 2$,则点 C 在点 A,B 之间
B.若 $n= 4$,则点 A 在点 B,C 之间
C.若 $n= 2$,则点 B 在点 A,C 之间
D.若 $n= 4$,则点 B 在点 A,C 之间
B
).A.若 $n= 2$,则点 C 在点 A,B 之间
B.若 $n= 4$,则点 A 在点 B,C 之间
C.若 $n= 2$,则点 B 在点 A,C 之间
D.若 $n= 4$,则点 B 在点 A,C 之间
答案:
B [解析]A.当n=2时,AC=2a+2,
∵AC+BC=2a+2+a+6=3a+8>AB=3a,
∴点C不在点A,B之间,故选项A错误;
[当AC+BC=AB时,点C在点A,B之间]
B.当n=4时,AC=4a+2,
∵AB+AC=3a+4a+2=7a+2,BC=a+6,
取正数a=$\frac{2}{3}$,则7a+2=$\frac{20}{3}$,a+6=$\frac{20}{3}$,
∴7a+2=a+6,
∴点A在点B,C之间,故选项B正确;
C.当n=2时,AC=2a+2,
∵AB+BC=3a+a+6=4a+6>AC=2a+2,
∴点B不在点A,C之间,故选项C错误;
D.当n=4时,AC=4a+2,
∵AB+BC=3a+a+6=4a+6>AC=4a+2,
∴点B不在点A,C之间,故选项D错误.故选B.
∵AC+BC=2a+2+a+6=3a+8>AB=3a,
∴点C不在点A,B之间,故选项A错误;
[当AC+BC=AB时,点C在点A,B之间]
B.当n=4时,AC=4a+2,
∵AB+AC=3a+4a+2=7a+2,BC=a+6,
取正数a=$\frac{2}{3}$,则7a+2=$\frac{20}{3}$,a+6=$\frac{20}{3}$,
∴7a+2=a+6,
∴点A在点B,C之间,故选项B正确;
C.当n=2时,AC=2a+2,
∵AB+BC=3a+a+6=4a+6>AC=2a+2,
∴点B不在点A,C之间,故选项C错误;
D.当n=4时,AC=4a+2,
∵AB+BC=3a+a+6=4a+6>AC=4a+2,
∴点B不在点A,C之间,故选项D错误.故选B.
7. 如图,点 C 是线段 AB 上一点,点 M,N,P 分别是线段 AC,BC,AB 的中点. 若 $AC= 3\ cm$,$CP= 1\ cm$,则线段 $PN= $
$\frac{3}{2}$
cm.
答案:
$\frac{3}{2}$ [解析]由题意知,AP=AC+CP=4cm
∵P为AB的中点,
∴AB=2AP=8cm.
∵AC=3cm,
∴BC=AB−AC=5cm.
∵N为BC的中点,
∴CN=$\frac{1}{2}$BC=$\frac{5}{2}$cm,
∴PN=CN−CP=$\frac{3}{2}$cm.
归纳总结 本题考查的是两点间距离的计算,掌握线段的中点的性质,灵活运用数形结合思想是解题的关键.
∵P为AB的中点,
∴AB=2AP=8cm.
∵AC=3cm,
∴BC=AB−AC=5cm.
∵N为BC的中点,
∴CN=$\frac{1}{2}$BC=$\frac{5}{2}$cm,
∴PN=CN−CP=$\frac{3}{2}$cm.
归纳总结 本题考查的是两点间距离的计算,掌握线段的中点的性质,灵活运用数形结合思想是解题的关键.
8. 分类讨论思想 如图,直线 l 上线段 $AB= 6$,线段 $CD= 2$(点 A 在点 B 的左侧,点 C 在点 D 的左侧),若线段 CD 的端点 C 从点 B 开始以 1 个单位长度/秒的速度向右运动,同时点 M 从点 A 开始以 2 个单位长度/秒的速度向右运动,点 N 是线段 BD 的中点,则线段 CD 运动______秒时,$MN= 2DN$.
]

]

2或18
答案:
2或18 [解析]设线段CD运动的时间为t秒,则AM=2t,BC=t,BD=BC+CD=t+2,AD=AB+BD=6+t+2=t+8.
∵点N是线段BD的中点,
∴BN=ND=$\frac{1}{2}$BD=$\frac{1}{2}$(t+2)=$\frac{1}{2}$t+1.
①当点M在点N左侧时,
MN=AD−AM−ND=(t+8)−2t−($\frac{1}{2}$t+1)=7−$\frac{3}{2}$t,2DN=BD=t+2.
∵MN=2DN,
∴7−$\frac{3}{2}$t=t+2,解得t=2.
②当M点在N点右侧时,
MN=AM−AB−BN=2t−6−($\frac{1}{2}$t+1)=$\frac{3}{2}$t−7,
2DN=BD=t+2.
∵MN=2DN,
∴$\frac{3}{2}$t−7=t+2,解得t=18.
综上所述,线段CD运动2秒或18秒时,MN=2DN.
易错警示 本题主要考查了线段的中点,线段的和、差,直线上的动点问题,解题的关键是正确地把各条线段用含有t的式子表示出来,并且注意分类讨论.
∵点N是线段BD的中点,
∴BN=ND=$\frac{1}{2}$BD=$\frac{1}{2}$(t+2)=$\frac{1}{2}$t+1.
①当点M在点N左侧时,
MN=AD−AM−ND=(t+8)−2t−($\frac{1}{2}$t+1)=7−$\frac{3}{2}$t,2DN=BD=t+2.
∵MN=2DN,
∴7−$\frac{3}{2}$t=t+2,解得t=2.
②当M点在N点右侧时,
MN=AM−AB−BN=2t−6−($\frac{1}{2}$t+1)=$\frac{3}{2}$t−7,
2DN=BD=t+2.
∵MN=2DN,
∴$\frac{3}{2}$t−7=t+2,解得t=18.
综上所述,线段CD运动2秒或18秒时,MN=2DN.
易错警示 本题主要考查了线段的中点,线段的和、差,直线上的动点问题,解题的关键是正确地把各条线段用含有t的式子表示出来,并且注意分类讨论.
9. 已知点 A,B,C 在同一条直线上,且 $AB= 7\ cm$,$BC= 4\ cm$. 若 D 是线段 AC 的中点,请画出图形并求 AD 的长.
答案:
有两种情况:
①如图
(1),当点C在线段AB的延长线上时,
[题中条件仅给出了线段长度,无法确定点C的具体位置,因此需分类讨论]
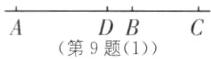
AD=$\frac{1}{2}$AC=$\frac{1}{2}$×(7+4)=5.5(cm);
②如图
(2),当点C在线段AB上时,

AD=$\frac{1}{2}$AC=$\frac{1}{2}$×(7−4)=1.5(cm).
故AD的长为5.5cm或1.5cm.
有两种情况:
①如图
(1),当点C在线段AB的延长线上时,
[题中条件仅给出了线段长度,无法确定点C的具体位置,因此需分类讨论]
AD=$\frac{1}{2}$AC=$\frac{1}{2}$×(7+4)=5.5(cm);
②如图
(2),当点C在线段AB上时,

AD=$\frac{1}{2}$AC=$\frac{1}{2}$×(7−4)=1.5(cm).
故AD的长为5.5cm或1.5cm.
查看更多完整答案,请扫码查看


